Section OAF Other Algebraic Functions
Introduction: Of all the functions that are studied, after linear and quadratic functions, there are two common class of functions that involve only the simple operations of addition, subtraction, multiplication and division. These are the classes of polynomial functions and rational functions.
The polynomial functions are characterized by the operations: finding whole number powers of a number. multiplication by a constant and addition of a constant or adding numbers combined by the previous list of operations. The rational functions are characterized by allowing further the operation of division of numbers that result from two polynomial functions as long as that is proper. [No division is allowed by $0$.] For example, the function defined by assigning the
value $f(x) =x^3 - 4 x $ to the number $x$, also
represented symbolically as $f: x \rightarrow x^3 - 4
x$ , or verbally by saying "to find
$f(x)$, cube $x$, then subtract $4x$ from
the result". $f$ is described as a cubic polynomial
function. This function is visualized by
the mapping diagram, OA1.
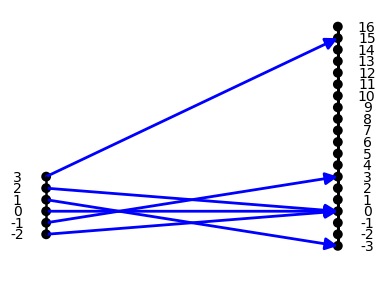
Mapping Diagram OA1
For a simple example of a rational function, we
can consider the function defined by assigning the value
$f(x) = \frac 2 x$ to the number $x \ne 0$, also
represented symbolically as $f: x \rightarrow \frac 2 x
$ , or verbally by saying "to find
$f(x)$, find the quotient of $2$ divided by $x$".
$f$ is described as a rational function. This
function is visualized by the mapping diagram,
OA2. Notice the arrow from $x=0$ does not
arrive at the target line to indicate the function
is not defined at $x=0$.
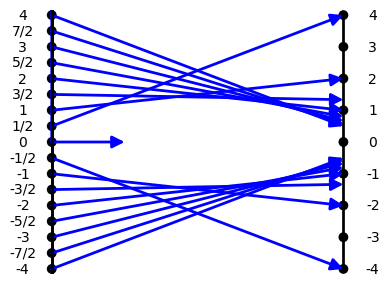
Mapping Diagram OA2
This section will provide examples, explanations, exercises and problems that will help students use the power of the mapping diagram along with the three other tools (equations, tables , and graphs) to understand these other algebraic functions and their inverses.
Polynomial Function Definition
Rational Function Definition
One very important result about polynomial is most useful throughout the analysis of algebraic functions. Though usually stated sometime during a second course in algebra, it is not proven until possibly in some upper division college course. We state it here in a form connected to polynomial functions:
OAF.FTAThe Fundamental Theorem of Algebra
OAF.OAFI Polynomial and Rational Functions are Important. (Not yet ready.)
This example presents the rational (linear
fractional) function $f(x) = \frac {x+1} {x-2} = 1
+ \frac 3 {x-2}$ with a table of data, a graph and
a mapping diagram.
[We have already seen examples of 2nd degree
polynomial (quadratic)
functions.]
Treatment of polynomial and rational functions and their graphical interpretation along with cubic and simple rational equations are often treated in algebra courses in preparation for calculus. [See wikipedia.org/wiki Cubic function. Rational_function]
What is missing is a balanced treatment using mapping diagrams to reinforce the function aspect of visualization. That will be emphasis of this section.
Comparisons will be made when appropriate to graphs- but we will develop the basic concepts for polynomial and rational functions with mapping diagrams. The end of this section includes some powerful and different ways to think about some of the most common of these functions and the ways they are represented algebraically.