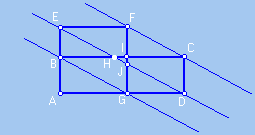
Of the equality of areas we have AB.AD = AE.AG, and therefore AD/AG=AE/AB.
From this we conclude that straight lines BG and ED are parallel segments,
and
therefore BEJG and GBHD are parallelograms ,
using
here the characterization of parallelogram in terms of parallel opposite
sides.
Also we have that FJDC is parallelogram.
 |
In fact: Since BEJG is a parallelogram, we have congruent sides EB and JG, and as EB is congruent to FI it follows, from transitivity, that FI is congruent to JG. We have then FJ congruent to IG, and consequently, is congruent to CD, which allows one to conclude that FJDC also is parallelogram , using here the characterization of parallelogram in terms of pair of parallel and congruent opposite sides. |
From the existence of these four parallelograms we conclude that the
segments are congruent:
* GD and BH, BE and GJ, and therefore triangles GDJ
and BHE are congruent;
* DC and JF, CH and FE, and therefore DCH
and JFE are congruent triangles.