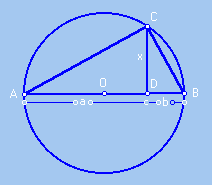
or either, the length CD is the square root of the product of
the lengths of CA and CB.
The square on the side CD has the same area as the rectangle with
sides a and b.
 |
The segment CD has as length the square root of a.b. In fact, the similarity
between triangles ACD and CBD (both of which are similar to the ABC triangle)
we have that:
or either, the length CD is the square root of the product of
the lengths of CA and CB.
|