1. Estimating Solutions to Parametric Differential Equations: A Predator-Prey Model.

Due  2-20 .
Read Section 10.7 of Stewart especially Example 1, parts a and b related to
 

Equation 1:  dR/dt = kR - aRW      dW/dt = -rW + bRW.
 

Read pages 624-626 on Euler's method together with materials from Flashman on Euler's method .
 

1. Suppose R(0)=100 and W(0)=10 in Equation 1. Estimate R(4) and W(4) using Euler's method with n = 4 with the following choices for the constants a,b,k, and r. In each case discuss the quality of your estimate and the relation of these to part a and b ot Example 1 of Stewart..
1. a = b = 1,  k = 2,  r  = .5 .
2. a = .2,  b =.5,  k = r = 1.

1. Curvature for graphs of functions in the plane.

Due 3-6 .
1. Paramatrize the graph of y = f(x) with x = t and y = f(t).

Use formula 9 on page 885 to prove that the curvature of the graph of f  at (x, f(x) is given by the formula k (x) = |f '' (x)| / [1 + (f'(x)²] ^3/2 .
2. Find where the graph of y = ln(x) has its largest curvature.

 
1. Due: 3-25    In  Stewart:

15.3: 70,72
15.4: 38

 
1. Homogeneous functions and the motion controlled by a heat seeking process.

Due 4-4
1. a. A real valued function of two variables, f::R²->R  is called homogeneous of degree m if for any real numbers x,y,and t,  f(tx,ty) = t ^m f(x,y). Suppose f is differentiable and homogeneous of degree m, show that  x D _x f(x,y) + y D _y f(x,y) = m f(x,y). [Hint: If g(t) = f(tx,ty) , find g'(1).]

   b. Generalize your result to homogeneous differentiable functions of 3 and 4 variables.

2. The temperature distribution on a metal plate at time t is given by the function H _t of x and y:

 H _t(x,y) = -[(x-cos( pt )) ² + (y-sin( pt )) ² ]. A manually controlled particle moves along the plate in straight lines periodically adjusting the direction vector of the line it follows so that at the time the direction is adjusted the new direction vector is in the direction of most rapid temperature increase at that instant and the particle has speed equal to that most rapid rate.
   a) Describe the motion of the particle if it is located at (0,0) when t=0 and adjustments are made when t = 0,1,2,3,4,... etc.
   b) Describe the motion of the particle if it is located at (0,0) when t=0 and adjustments are made when t = 0,1/2,1,3/2,2,... etc.

---


 
2. Extremes of linear functions on triangular regions. Due 4-11-03

Suppose T is a triangular region in the plane.
Suppose L(x,y) = Ax + By where A and B are constants that are not both 0.
Use the LaGrange theory to explain why the maximum (or minimum ) values of L for the region T will occur at one of the  vertices of the triangle.

State and justify the analogous result for planar regions bounded by quadrilaterals and pentagons.
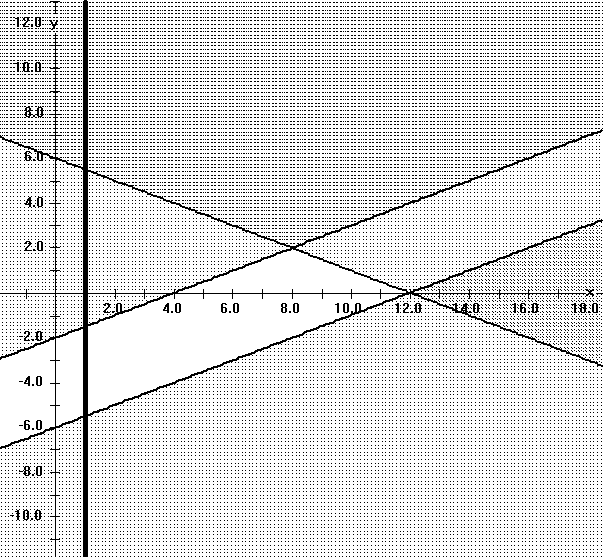
Apply this work to find the maximum and minimum values of L(x,y) = 3x + 5y when (x,y) satisfy all the following (linear) inequalities:

 x - 2y  < = 12;
12 > =   x + 2 y;
4 < =  x- 2y ;
and 1 < =  x.


3 Bonus Points:  Generalize this problem to one of the following situations:
        a.  A tetrahedron in space with L(x, y, z) = Ax + By + Cz with A,B, and C not all 0.
        b.  A planar region bounded by a polygon with n sides.
Justify your statement and illustrate it with an example.

---


 
3. Independent Factors in Products. Due

A. Find òò_R  (3x²+1) (4y³ +2y +1) dA where R = [1,3] × [0,2].
B. Suppose g and h are continuous real valued functions of one variable.
Let F(x,y) = g(x)h(y). Explain why òò_R F(x,y) dA = ò_a^b g(x) dx  ò_c^d h(y) dy  where R = [a,b] × [c,d].
C. Use part B to show that  òò_R exp(-x² - y²) dA = [ò_-m^m exp(-x²) dx]²   where R = [-m,m] × [-m,m] .