- Show that g takes on its smallest value when `A = 1/pi int_{-pi}^pi f(x) sin(x) dx` .
-
Find the values of A that minimize g(A) in part i)
a) when f(x) = x and
b) when f(x) = ex
-
Due 11/2 Some Integrals
.
a) Find `int {tan^{-1}(x)}/( 1+x^2 ) dx`.
b) Find `int x^3 sin(x) dx`.
c) Find `int (x^3+3x^2+1)/( x^3+x^2+x+1 ) dx`.
d) Find `int_1^e [ln(x)]^3 dx`.
-
Due 11/23 .
Differential Equations, MacLaurin Polynomials, and Euler's Method.
-
Suppose f is a "`C^{oo}` "
function with f (0) = 1, f '(0) = -1 and f ''(x)=
2f '(x) + 3f (x).
-
Find the MacLaurin polynomial of degree
6 for f.[Hint: First find an equation for f '''(x).]
-
Estimate the value of f (1) using
this polynomial.
-
Use Euler's method with n = 4 to estimate
f
(1).
-
Let `g(x) = (1+x)^{1/2}` . Find the Maclaurin polynomial of
degree 4 for `g`. Use your result to estimate `g(1)`. Discuss the error in
this estimate.
-
....
-
Find the Maclaurin polynomial of degree 8 for `cos 2x`.
-
Find the Maclaurin polynomial of degree 8 for `sin ^2 x`. (Hint:`sin^2 x = (1 - cos (2x) )/2`.)
-
Estimate `int_0^1 ({sin (x)} /x )^2 dx` using the first three non-zero terms
of the Maclaurin polynomial in ii). Explain how you handled the fact that
this is an improper integral in your estimate.
-
Estimate the integral in part iii) using Simpson's rule. Explain how you
handled the fact that this is an improper integral in your estimate.
Discuss the error in your estimate in part iii). [Use Taylor's theorem.]
-
Due . A
very flat function:
Let f(x) = exp(-1/x 2 ) when
x is not 0 and f(0)=0.
a) Explain why f is continuous at x = 0.
b) Find f '(x) when x is not 0.
c) Find f '(0). (Hint: Use the def'n of the derivative and L'Hospital's
Rule.)
d) Find f ''(x) when x is not 0.
e) Find f ''(0).(Hint: Use the def'n of the derivative and L'Hospital's
Rule.)
f) Sketch the graph of f.
g) Show that f '''(0) = 0 .
-
Due: Probability
Find exactly or estimate the value of a > 0 so that f
(x)
= e - 2x is a probability density function of a random
variable on the interval [-a, a].
Determine the mean for this random variable.
-
Due: Estimating functions and integrals.
Often information about a function is limited to the value of the function
at a few points or the values of the function and some of its derivatives
at a single point. The following problems ask you to construct alternative
functions matching the same given information and compute related
integrals.
1. Suppose f is a function with f (0) = 0, f (1) = 1, and f (2)
= 0 .
A Find a trigonometric function trig(x) so that trig(0) = f (0)
= 0, trig(1) = f (1) = 1, and trig(2) = f (2) = 0.
Graph the function trig and find 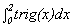 .
.
B. Find a quadratic polynomial function q(x) so that q(0) = f (0) =
0, q(1) = f (1) = 1, and q(2) = f (2) = 0.
Graph the function q and find 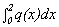 .
.
2. Suppose f is a function with f (0) = 1, f '(0) = 1, and f
''(0) = -1 .
A. Find a trigonometric function rig(x) so that trig(0) = f(0) = 1,
trig '(0) = f '(0) = 1, and trig ''(0) = f ''(0) = -1.
Graph the function trig and find 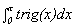 .
.
B. Find a quadratic polynomial function q(x) so that q(0) = f(0)
=1, q '(0) = f '(0) = 1, and q ''(0) = f ''(0) = -1.
Graph the function q and find 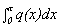 .
.
3. Suppose f is a function with f (0) = 1, f '(0) = 1, f ''(0)
= 1, f '''(0) = 1, and f ''''(0)=1.
A. Find a quadratic polynomial function q(x) so that q(0) = f(0)
= 1, q '(0) = f '(0) = 1, and q ''(0) = f ''(0) = 1.
Graph the function q and find 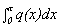 .
.
B.Find a cubic polynomial function c(x) so that c(0) = f(0) = 1, c
'(0) = f '(0) = 1, c ''(0) = f ''(0) = 1, and c '''(0) = f '''(0) = 1.
Graph the function c and find  .
.
C. Find a quartic polynomial function r(x) so that r(0) = f(0) = 1,
r '(0) = f '(0) = 1, r ''(0) = f ''(0) = 1, r '''(0) = f '''(0) =
1, and r ''''(0) = f ''''(0) = 1.
Graph the function r and find 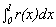 .
.
-
Due: .
Comparing
Functions and Polynomials.
One way to select a polynomial to use for approximating a non-polynomial
function is to select coefficients for the polynomial to minimize some
measure of the difference between the two functions.
-
---
-
Find the value(s) for the coefficient m of a linear function f(x)
= mx to minimize the largest difference between f(x) and the function
p(x)
= x2 for all x in the interval [0,1]. Explain
your result. Draw a figure showing the point between 0 and 1 where the
difference is largest.
-
Find the value(s) for the coefficient m of a linear function f(x)
= mx to minimize the largest difference between f(x) and the function
p(x)
= x3 for all x in the interval [0,1]. Explain your
result. Draw a figure showing the point between 0 and 1 where the difference
is largest.
-
What if p(x)= xn where n is
a positive integer?
-
What if p(x) = ex -1 ?
-
What can you say in general about this problem?
-
---
-
Find the value(s) for the coefficient m of a linear function f(x)
= mx to minimize the value of the definite integral,
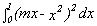 . Explain your result.
. Explain your result.
-
Find the value(s) for the coefficient m of a linear function f(x)
= mx to minimize the value of the definite integral,
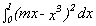 . Explain your result.
. Explain your result.
-
What if the integral is
 where n is a positive integer?
where n is a positive integer?
-
What if the integral is
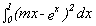 ?
?
 1
1