- Darts: Imagine a circular board of radius 60 centimeters which is a powerful magnet. See Figure 1. This magnet is very strong so that when I turn my back to it and release a magnetic dart, the dart will be drawn to the board and will land at random somewhere on the board. Let's suppose for simplicity the following uniformity condition:
-
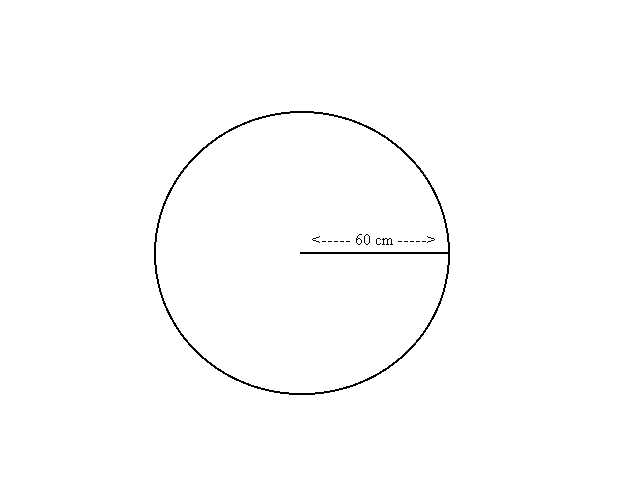 If the board is divided into two regions by a concentric circle of radius
30 and I repeat the experiment a large number of times, what proportion
of markings from the experiment is likely to lie in the inner region?
See Figure 1.
If the board is divided into two regions by a concentric circle of radius
30 and I repeat the experiment a large number of times, what proportion
of markings from the experiment is likely to lie in the inner region?
See Figure 1. - If the board is divided into four regions by concentric circles of radius 15, 30, and 45 cm and I repeat the experiment a large number of times, what proportion of the markings from the experiments is likely to lie in each of the regions?
- If the board is divided into n regions by concentric circles of radius
(k/n) 60 cms with k = 1,2 ... n-1, and I repeat the experiment a large
number of times, what proportion of the markings from the experiments
is likely to lie in each of the regions?
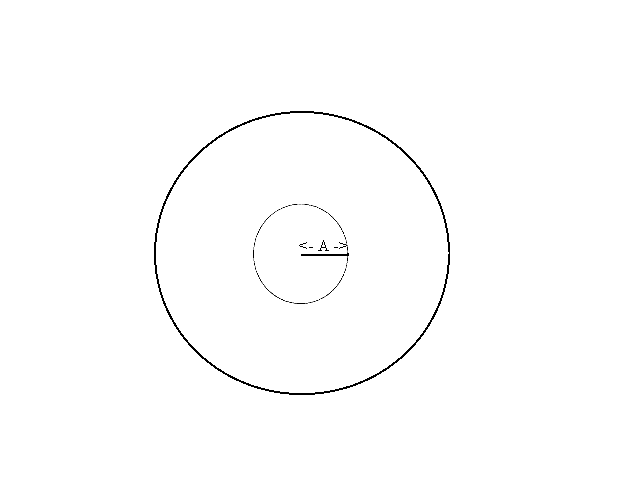
- What proportion of the markings from repeating the experiment is likely for the dart to lie within A cms of the center where 60>A>0? See Figure 2
- Darts and Averages. Consider the same circular magnetic dart board with radius 60 centimeters. Draw 5 concentric circles on the board with radii 10,20,30,40, and 50 creating 6 regions (one disc and five bands). Consider the following game: Throw the dart at the board and score 5 points for landing in the inner disc, 15 points for landing in the smallest band (between the circles of radius 10 and 20), 25 points for landing in the next smallest band (between the circles of radius 20 and 30), 35 points for landing in the band between the circles of radius 30 and 40, 45 points for landing in the band between the circles of radius 40 and 50, and 55 points for landing in the outermost band (between the circle of radius 50 and and the edge of the dart board). [In this game a low score is considered evidence of greater skill.]
If we have any two regions on the board of equal area then the dart would land in those regions about the same number of times with a large number of throws.
In other words the two events of the dart falling in two regions of equal area are equally probable or equi-likely. Now I'll throw a magnetic dart and mark where it lands on the board. This is our basic experiment. For each of the following questions include a discussion of how you arrived at your answer with your response.
We allow a player to throw a dart 36 times and find the total score
for the player as well as the average score (the total divided by 36).
Notice the average will be a number between 5 and 55. Give a total score
and an average that are likely for a player with no special skill. [These
numbers are described as the expected score and the expected average for
the game.] Discuss your reasoning and show the work leading to your proposed
solution.
Suggestion: You might investigate the similar problem with 2 regions
and 4 throws and then 4 regions and 16 throws as a way to begin thinking
about the problem. How many darts do you think would fall in each region?
If we measure the distance each of the 36 darts fall from the center, what do you think the average distance would be for a player with no special skills. Explain your reasoning, any connections with the expected average score in the game, and whether you have any belief about the accuracy of your response. (Is it an underestimate or an overestimate?)
The sine function satisfies the differential equation y'' = -y. In other words, if y = f(x) and y' = f '(x) = g(x), and g'(x) = - f(x) with y(0) = f (0) = 0 and y'(0) = g(0) = 1 then a solution for y is y(x) = f(x) = sin(x). We can therefore apply Euler's method in estimating the sine as the solution to the differential equation y'' = -y with the initial conditions y(0) = 0 and y'(0) = 1.
The tangent function satisfies the differential equation y' =
1+y 2 with y(0)=0. This allows us to estimate
the tangent function with Euler's method as the solution to this differential
equation.
- Use Euler's method with n = 10 applied to y'' = -y with the initial conditions y(0) = 0 and y'(0) = 1 to estimate sin(1). Compare your result to the value for sin(1) on your calculator. [Understimate? overestimate? why?]
- Use Euler's method with n = 10 applied to y'' = -y with the initial conditions y(0) = 1 and y'(0) = 0 to estimate cos(1).Compare your result to the value for cos(1) on your calculator. [Understimate? overestimate? why?]
- Use the previous estimates to estimate tan(1).
-
Use Euler's method with n = 10 applied to y' = 1+y 2
with y(0)=0 to estimate tan(1). Compare your result to the value
for tan(1) on your calculator. [Understimate? overestimate? why?]
Often information about a function is limited to the value of the function at a few points or the values of the function and some of its derivatives at a single point. The following problems ask you to construct alternative functions matching the same given information and compute related integrals.
1. Suppose f is a function with f (0) = 0, f (1) = 1, and f (2)
= 0 .
A Find a trigonometric function trig(x) so that trig(0) = f (0)
= 0, trig(1) = f (1) = 1, and trig(2) = f (2) = 0.
Graph the function trig and find ![]() .
.
B. Find a quadratic polynomial function q(x) so that q(0) = f (0) =
0, q(1) = f (1) = 1, and q(2) = f (2) = 0.
Graph the function q and find ![]() .
.
2. Suppose f is a function with f (0) = 1, f '(0) = 1, and f
''(0) = -1 .
A. Find a trigonometric function rig(x) so that trig(0) = f(0) = 1,
trig '(0) = f '(0) = 1, and trig ''(0) = f ''(0) = -1.
Graph the function trig and find ![]() .
.
B. Find a quadratic polynomial function q(x) so that q(0) = f(0)
= 1, q '(0) = f '(0) = 1, and q ''(0) = f ''(0) = -1.
Graph the function q and find ![]() .
.
3. Suppose f is a function with f (0) = 1, f '(0) = 1, f ''(0)
= 1, f '''(0) = 1, and f ''''(0)=1.
A. Find a quadratic polynomial function q(x) so that q(0) = f(0)
= 1, q '(0) = f '(0) = 1, and q ''(0) = f ''(0) = 1.
Graph the function q and find ![]() .
.
B.Find a cubic polynomial function c(x) so that c(0) = f(0) = 1, c
'(0) = f '(0) = 1, c ''(0) = f ''(0) = 1, and c '''(0) = f '''(0) = 1.
Graph the function c and find ![]() .
.
C. Find a quartic polynomial function r(x) so that r(0) = f(0) = 1,
r '(0) = f '(0) = 1, r ''(0) = f ''(0) = 1, r '''(0) = f '''(0) =
1, and r ''''(0) = f ''''(0) = 1.
Graph the function r and find ![]() .
.
-
Let
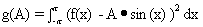 .
. -
Show that g takes on its smallest value when
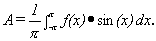
- Find the values of A that minimize g(A) in part a)
- FOR THIS PROBLEM ASSUME f '(x) = g(x) and g'(x)= f(x) for all x, and that f(0) = 0 and g(0) = 1.
- Using Euler's method with n = 4, estimate f(1) and g(1).
- Show that [g(x)] 2 - [f(x)] 2=1 for all x. [Hint: Consider P(x)=[g(x)] 2 - [f(x)] 2.]
-
Let
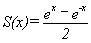 .
Show S''(x) = S(x), S(0) = 0 and S'(0) = 1.
.
Show S''(x) = S(x), S(0) = 0 and S'(0) = 1. - Using your knowledge of calculus and the exponential function, graph the following:
(a) S(x). (b) S'(x).
In your graphs show and explain such features as extrema, concavity, symmetry, etc.
a) Find
b) Find .
c) Find
.
d) Find
.
One way to select a polynomial to use for approximating a non-polynomial function is to select coefficients for the polynomial to minimize some measure of the difference between the two functions.
- ---
- Find the value(s) for the coefficient m of a linear function f(x) = mx to minimize the largest difference between f(x) and the function p(x) = x2 for all x in the interval [0,1]. Explain your result. Draw a figure showing the point between 0 and 1 where the difference is largest.
- Find the value(s) for the coefficient m of a linear function f(x) = mx to minimize the largest difference between f(x) and the function p(x) = x3 for all x in the interval [0,1]. Explain your result. Draw a figure showing the point between 0 and 1 where the difference is largest.
- What if p(x)= xn where n is a positive integer?
- What if p(x) = ex -1 ?
- What can you say in general about this problem?
- ---
-
Find the value(s) for the coefficient m of a linear function f(x)
= mx to minimize the value of the definite integral,
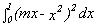 . Explain your result.
. Explain your result. -
Find the value(s) for the coefficient m of a linear function f(x)
= mx to minimize the value of the definite integral,
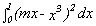 . Explain your result.
. Explain your result. -
What if the integral is
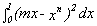 where n is a positive integer?
where n is a positive integer? -
What if the integral is
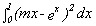 ?
?
-
Suppose f is a
 function with f (0) = 1, f '(0) = -1 and f ''(x)=
2f '(x) + 3f (x).
function with f (0) = 1, f '(0) = -1 and f ''(x)=
2f '(x) + 3f (x). - Find the MacLaurin polynomial of degree 6 for f.[Hint: First find an equation for f '''(x).]
- Estimate the value of f (1) using this polynomial.
- Use Euler's method with n = 4 to estimate f (1).
- Let g(x) = (1+x)1/2 . Find the Maclaurin polynomial of degree 4 for g. Use your result to estimate g(1). Discuss the error in this estimate.
- ....
- Find the Maclaurin polynomial of degree 8 for cos 2x.
- Find the Maclaurin polynomial of degree 8 for sin 2x. (Hint: sin 2 x = (1 - cos (2x) )/2.)
- Estimate òx=0 x=1(sin (x) /x )2 dx using the first three non-zero terms of the Maclaurin polynomial in b). Explain how you handled the fact that this is an improper integral in your estimate.
- Estimate the integral in part c) using Simpson's rule. Explain how you handled the fact that this is an improper integral in your estimate.
- Discuss the error in your estimate in part iii). [Use Taylor's theorem.]
- A very flat function:
Let f(x) = exp(-1/x 2 ) when x is not 0 and f(0)=0.
a) Explain why f is continuous at x = 0.
b) Find f '(x) when x is not 0.
c) Find f '(0). (Hint: Use the def'n of the derivative and L'Hospital's Rule.)
d) Find f ''(x) when x is not 0.
e) Find f ''(0).(Hint: Use the def'n of the derivative and L'Hospital's Rule.)
f) Sketch the graph of f.
g) Show that f '''(0) = 0 .