• If we have any two regions on the board of equal area then the dart would land in those regions about the same number of times with a large number of throws.

(a) If the board is divided into two regions by a concentric circle of radius 30 and I repeat the experiment a large number of times, what proportion of markings from the experiment is likely to lie in the inner region? See Figure 1 .
(b) If the board is divided into four regions by concentric circles of radius 15, 30, and 45 cm and I repeat the experiment a large number of times, what proportion of the markings from the experiments is likely to lie in each of the regions?
(c) If the board is divided into n regions by concentric circles of radius  k * 60/n cms with k = 1,2 ... n-1, and I repeat the experiment a large number of times, what proportion of the markings from the experiments is likely in each of the regions? 
(d) What proportion of the markings from repeating the experiment is likely for the dart to fall within A cms of the center where 0<A<60?

2. Darts and Averages. Consider the same circular magnetic dart board with radius 60 centimeters. Draw 5 concentric circles on the board with radii 10,20,30,40, and 50 creating 6 regions (one disc and five bands). Consider the following game: Throw the dart at the board and score 5 points for landing in the inner disc, 15 points for landing in the smallest band (between the circles of radius 10 and 20), 25 points for landing in the next smallest band (between the circles of radius 20 and 30), 35 points for landing in the band  between the circles of radius 30 and 40, 45 points for landing in the band between the circles of radius 40 and 50, and 55 points for landing in the outermost band (between the circle of radius 50 and the edge of the dart board). [In this game a low score is considered evidence of greater skill.]

We allow a player to throw a dart 36 times and find the total score for the player as well as the average score (the total divided by 36). Notice the average will be a number between 5 and 55.
Give a total score and an average that are likely for a player with no special skill. [These numbers are described as the expected score and the expected average for the game.]
Discuss your reasoning and show the work leading to your proposed solution.

Suggestion: You might investigate the similar problem with 2 regions and 4 throws and then 4 regions and 16 throws as a way to begin thinking about the problem. How many darts do you think would fall in each region?
Extension: (Optional) If we measure the distance each of the 36 darts fall from the center, what do you think the average distance would be for a player with no special skills.  Explain your reasoning, any connections with the expected average score in the game, and whether you have any belief about the accuracy of your response. (Is it an underestimate or an overestimate?)

One way to make a curve that passes through several points and looks smooth is to draw several curves that are defined by a small number of points and make sure that when the curves are joined together they have the same tangent lines, making

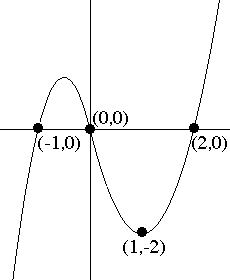
A. Use two curves defined by quadratic functions to make a single smooth curve that passes through the four points, (-1,0), (0,0), (1,-2) and (2,0) as in the figure. Discuss briefly the strategy you used to find your solution.

Suggestion: Let f(x) = Ax² + Bx + C  and g(x) = Ex² + Fx + G  . Have the pair of curves meet at (0,0).

B. Find a second pair of quadratic polynomials which can be used to make a single smooth curve that passes through the same four points.

C. Find a single cubic polynomial that passes through the same four points.

D. Use some technology to sketch your solutions for A,B, and C. Discuss briefly any noticeable differences (such as "vertices") between the three curves.

3. Due Friday 10-27-00
A. Tan page 367 # 24.
B. Tan page 370 # 38
 

4. Due Tuesday 11-14-00
A. Tan  page 434 #16
B. Tan page 437 #42

5. Due Tuesday 12-5-00
A. Tan  page 452 #68
B. Tan page 453 #7699