|
translation |
horizontal |
vertical |
|
reflection + |
glide |
rotation |
reflection + |
|
translation |
horizontal |
vertical |
|
reflection + |
glide |
rotation |
reflection + |
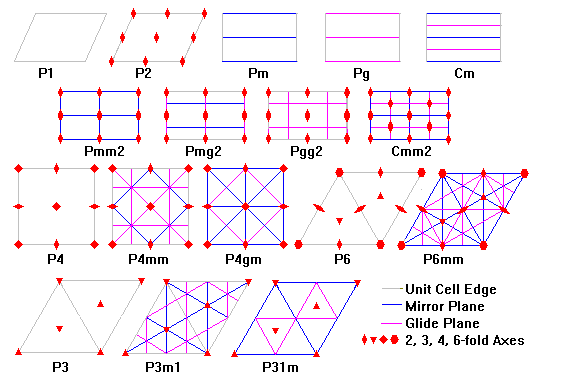
 translations |
 reflections |

reflections + |

glide |

reflections + |
 rotations (2) |
reflections + |
rotations (2) + |

rotations (2) + |
 rotations (4) |

reflections + |

rotations (4) + |
 rotations (3) |

reflections + |

rotations (3) + |
 rotations (6) |

reflections + |
Classification of IsometriesRigid Motions in (or about) the plane. Also called "Isometries" Orientation preserving Translations Rotations Orientation reversing Reflections Glide reflections
Next Class...Video : Isometries