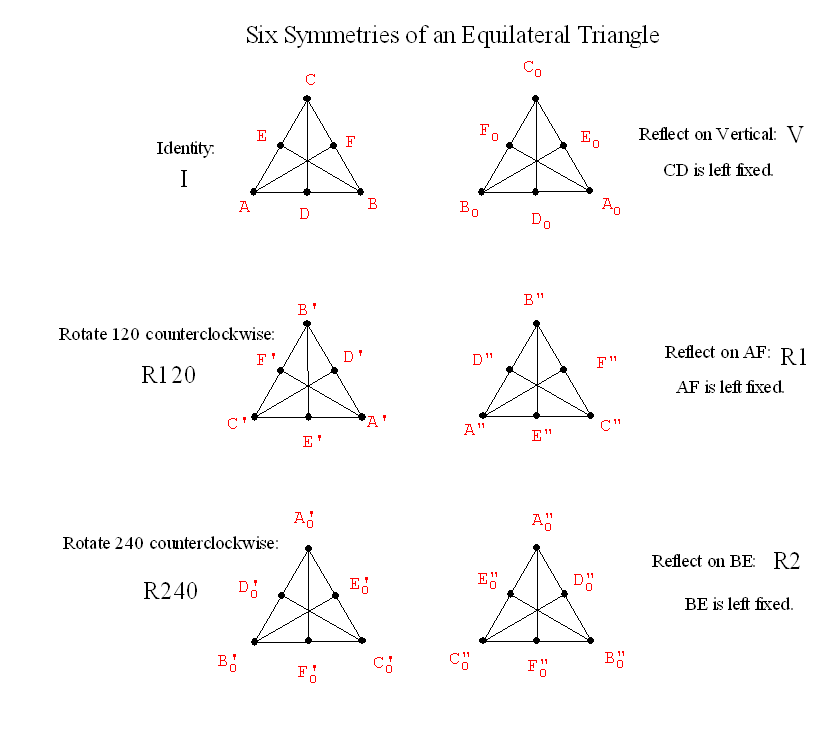
Recall Symmetries of an equilateral triangle:

In general: the sum of the interior angles in a n sided polygon is
A regular polygon is a polygon where the sides are all of equal length and the angles are all congruent (or of equal measure).
| name of polygon | n |
degrees of the interior measure of each angle |
360 degrees divided by # in Column 2 |
| equilateral triangle | 3 |
60 | 360 / 3 = 120 |
| square | 4 |
90 | 360/4= 90 |
| regular pentagon | 5 |
3*180/5= 108 |
360/5= 72 |
| regular hexagon | 6 |
4*180/6=120 |
360/6= 60 |
| regular heptagon | 7 |
5*180/7 |
360/7 |
| regular octagon | 8 |
6*180/8=135 |
360/8 = 45 |
| regular dodecagon |
12 |
10*180/12=1800/12=150
|
360/12=30 |

| * |
Id |
R120 |
R240 |
V |
G=R1 |
H=R2 |
| Id |
I |
|||||
| R120 |
R240 |
R1 |
||||
| R240 |
I |
R2 |
||||
| V |
R2 |
R1 |
I |
R120 |
||
| G=R1 |
I |
|||||
| H=R2 |
I |