Thursday September 15
-
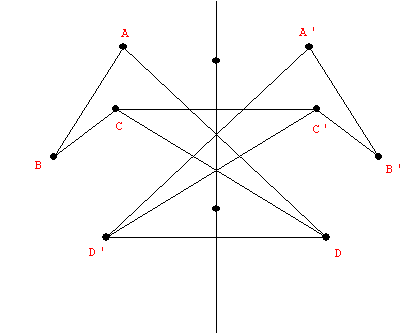
Symmetry Ideas
- Reflective symmetry: BI LATERAL SYMMETRY
T C O
0 I A
- Folding line: "axis of symmetry"
- The "flip."
- The "mirror."
-
- R(P) = P' : A Transformation. Before: P ....
After : P'
- If P is
on the line (axis), then R(P)=P. "P remains fixed by the reflection."
- If P is not on the axis, then the line PP' is
perpendicular to the axis and if Q is the point of intersection of PP' with
the axis then m(PQ) = m(p'Q).
- Definition: We say F has a reflective symmetry wrt a line l if there is a reflection
R about the line l where
R(P)=P' is still an element of F for every P in F....i.e.. R (F) = F.
l is called the axis of symmetry.
- Examples of reflective symmetry:
Squares... People
-
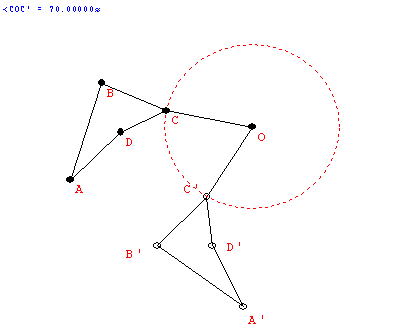
- Rotational Symmetry.
- Center of rotation. "rotational pole" (usually O)
and angle/direction of rotation.
- The "spin."
-
- R(P) = P' : A transformation
- If O is the center then R(O) = O.
- If the angle is 360 then R(P) = P for all P....
called the identity transformation.
- If the angle is between 0 and 360 then only
the center remains fixed.
- For any point P the angle POP' is the same.
- Examples of rotational symmetry.
- Now... what about finding all the reflective
and rotational symmetries of a single figure?
- Symmetries of playing card.... classify the cards by
having same symmetries.
Notice symmetry of clubs, diamonds,
hearts, spades
-
- Preview ... Possible tiles and tilings.
- One Regular Convex Polygon.
- Two or more Regular Convex Polygons.
- Other Polygon Tilings.
- Non polygonal tilings.
REVIEW: Recall our previous discussions for
a polygon with n sides.
When n = 3 this is a triangle, n=4, a quadrilateral, or
when n= 5, a pentagon.
The sum of the measures of the
interior angles of a triangle is 180 degrees.
Review Question:What about a quadrilateral? and a pentagon?
or an n sided polygon ( an "n -gon")?
From the figure we saw that for a quadrilateral (n =4), which can be dissected
into two triangles,
the sum is 2*180= 360 degrees.
And for a pentagon (n=5)
which can be dissected into 3 triangles, the sum is 3*180=540 degrees.
In general: the sum
of the interior angles in a n sided polygon
is
(n-2) *180 degrees.
A regular polygon
is a polygon where the sides are all of equal length
and the angles are all congruent (or of equal measure).
Review Question: what is the measure of an individual
angle in a regular polygon with n sides?
For a triangle, the individual angle is 180/3
= 60 degrees.
For a square, the individual angle is 360/4=90
degrees.
For a regular pentagon.... 3*180/5 = 540/5
=108 degrees.
Now for a HEXAGON (6 sides) the sum of the angles
is 720 degrees.
So ... for a REGULAR HEXAGON,
the individual angle is 4*180/6 =720/6 =120 degrees.
In general: The individual
angle for a regular polygon with n sides is (n-2)*180/n degrees.
This can be expressed in other ways using algebra:
(n-2)*180/n = [180 n - 360] / n = 180 - 360/n.
| name of polygon |
|
degrees of the interior
measure of each angle |
360 degrees divided
by # in Column 2 |
| equilateral triangle |
3
|
60 |
360 / 3 = 120 |
| square |
4
|
90 |
360/4= 90
|
| regular pentagon |
5
|
3*180/5= 108
|
360/5= 72
|
| regular hexagon |
6
|
4*180/6=120
|
360/6= 60
|
| regular heptagon |
7
|
5*180/7
|
360/7
|
| regular octagon |
8
|
6*180/8=135
|
360/8 = 45
|
regular dodecagon
|
12
|
10*180/12=1800/12=150
|
360/12=30
|
- Dissection of the plane--- Tilings
of the plane.
- One polygonal Tile: Quadrilateral Activity.
-
An on-line tool for making tilings of the plane
- Regular and semiregular Tilings of the plane.
- A tiling is a regular tiling if(i)it has a single tile shape that
is a regular polygon and (ii) the vertices and edges of the tiles coincide
(no overlapping edges)
- A tiling is a semi-regular tiling if (ii) each tile shape is a regular
polygon, (ii) the vertices and edges of the tiles coincide (no overlapping
edges) and (iii) every vertex has the same polygon types arranged around
it.
- Wingeometry download!
and demonstrate tesselations.
- Naming tilings
(Math Forum)
- The numbers represent the number of sides in the poygons.
- The order indcates the order in which the poygons are arranged about
a vertex.
- Local considerations about a vertex. The sum of the
angles must equal 360 degrees.
- 4.1 Ex. 3. How many tiles around single vertex:
3,4,5,6,7,8?...
- How can there be 6? Only one way: 3-3-3-3-3-3
(6*60= 360)
- Why not 7? If 7 or more tiles aroung a single
vertex the sum of the angles must exceed 360 degrees.
- 4.1 Ex. 4. Can there be 4 different tiles
around a single vertex? Not if they are all different since 60+90+108+120
= 378 >360.
- 4.1 Ex. 5. If there are 4 tiles around a
vertex then ....At least two of the tiles must have the same number of sides.
- Arithmetic for vertices.
Example: Three regular polygons about a vertex with
n , k, and p sides.(180 - 360/n) + (180 - 360/k) + (180
- 360/p) = 360
3*180 -360( 1/n+1/k+1/p)= 2*180
1*180 = 360( 1/n+1/k+1/p)
SO....
180/360 = 1/n + 1/k + 1/p
or
1/n + 1/k +
1/p=1/2
So, for example, n=3, k=4
and p= 5 is not possible since
1/3+1/4+1/5
>1/2.
Number of polygons
around a vertex |
Equation for angle sum = 360 |
Equivalent Arithmetic equation |
Solutions to the arithmetic equations. |
|
| 3: n , k, p |
180 - 360/n+180 - 360/k+180 - 360/p = 360 |
1/n+1/k+1/p =1/2 |
| 6 |
6 |
6 |
| 5 |
5 |
10 |
| 4 |
5 |
20 |
| 4 |
6 |
12 |
| 4 |
8 |
8 |
| 3 |
7 |
42 |
| 3 |
8 |
24 |
| 3 |
9 |
18 |
| 3 |
10 |
15 |
| 3 |
12 |
12 |
|
|
| 4: n, k, p, z |
180 - 360/n+180 - 360/k+180 - 360/p 180 - 360/z
= 360 |
1/n+1/k+1/p +1/z =2/2 =1 |
| 4 |
4 |
4 |
4 |
| 3 |
3 |
4 |
12 |
| 3 |
3 |
6 |
6 |
| 3 |
4 |
4 |
6 |
|
|
| 5: n, k, p, z, w |
180 - 360/n+180 - 360/k+180 - 360/p+180 - 360/z+180
- 360/w = 360 |
1/n+1/k+1/p +1/z+1/w =3/2 |
|
|
- Local consideration about a polygon:
- Examples: If there is an equilateral triangle involved
with 2 other polygons, then the other two ploygons must have the same number
of sides. Because: if there were two different polygons aroung the triangle,
then on vertex would not have all three polygons sharing that vertex. (such
as 3-10-15)
- Similar considerations can eliminate tilings using a single
pentagon and two other distinct tiles. (such as 4-5-20).
- Semiregular Tilings: global results!
Look at the results using wingeometry.
- Student lesson
(Math Forum) a place for further explorations on-line.