"minimal surfaces" (FAPP video)
Transforming surfaces: "turning the sphere inside out." video


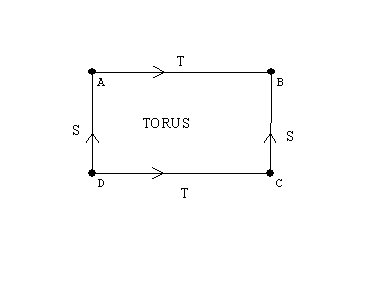
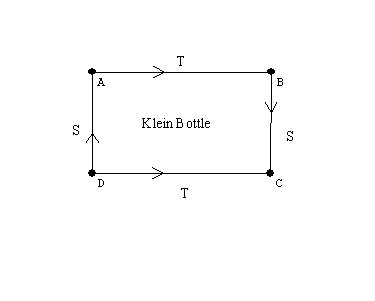
Non-orientable Surfaces and the fourth dimension
Thinking about a fourth (and higher) dimension:
A progression: Point and segment on a line, line segment and square in a plane (2-dim), square and a cube in space (3-dim), cube and a "hypercube" in hyperspace (4-dim)
The Hypercube and coordinates:
What do we measure? How does this determine "dimension?"
For a Line segment we can use one number to indicate distance and direction from a single point: 0 .... 1
For a Square we use two "coordinates" and we can identify the vertices of the square: (0,0), (1,0), (0,1),(1,1)
For a Cube we use three "coordinates" and we can identify the vertices of the cube with qualities such as "left..right", "up... down", and "front ... back":
(0,0,0) , (1,0,0), (0,1,0),(1,1,0)
(0,0,1), (1,0,1), (0,1,1), (1,1,1)
For a Hypercube....we use four "coordinates" and we can identify the vertices of the hypercube with qualities such as "left..right", "up... down", and "front ... back" and "inside... outside": (0,0,0,0) , (1,0,0,0), (0,1,0,0),(1,1,0,0)
(0,0,1,0), (1,0,1,0), (0,1,1,0), (1,1,1,0)
(0,0,0,1) , (1,0,0,1), (0,1,0,1),(1,1,0,1)
(0,0,1,1), (1,0,1,1), (0,1,1,1), (1,1,1,1)
Another four dimensional object:
The hyper simplex!

point
line segment
triangle
tetrahedron ("simplex")
Cards and the fourth dimension.
(clubs,diamonds,hearts,spades)
(1,1,1,1) (0,0,0,0)
(1,1,0,1) (0,0,1,0)
(0,1,0,1) (1,0,1,0)
(0,0,0,1) (1,1,1,0)
(0,0,0,0) (1,1,1,1)
Hamiltonian Tour: move through each vertex once and only once.
13 cards : (5,3,0,5) (4,2,6,1)
 Tradtional red/green 3D,
Tradtional red/green 3D,