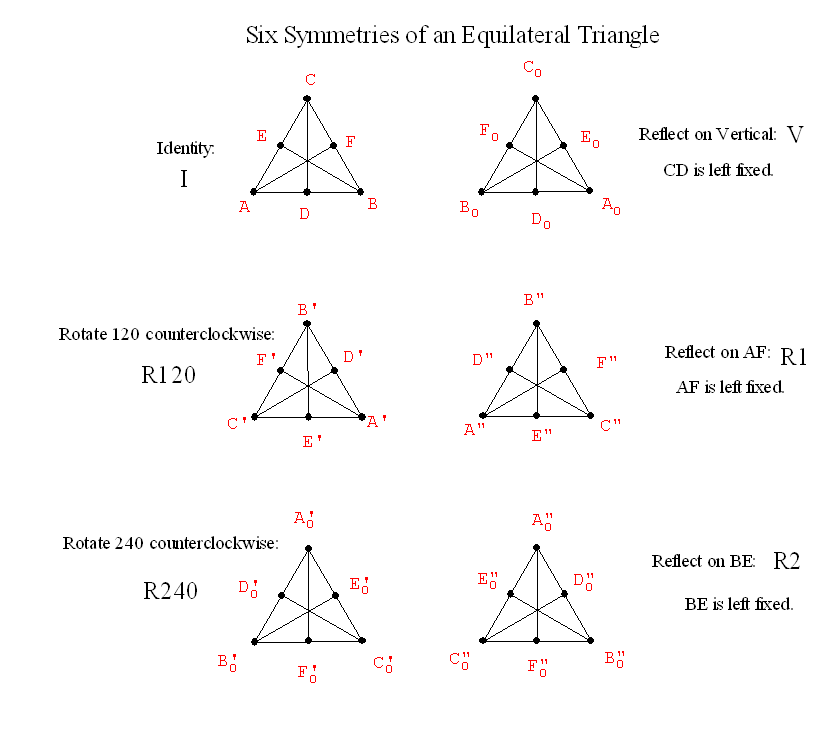

| * |
Id |
R120 |
R240 |
V |
G=R1 |
H=R2 |
| Id |
I |
|||||
| R120 |
R240 |
R2 |
||||
| R240 |
I |
R1 |
||||
| V |
R1 |
R2 |
I |
R120 |
||
| G=R1 |
I |
|||||
| H=R2 |
I |
| translation |
horizontal |
vertical |
| reflection + |
glide |
rotation |
reflection + |
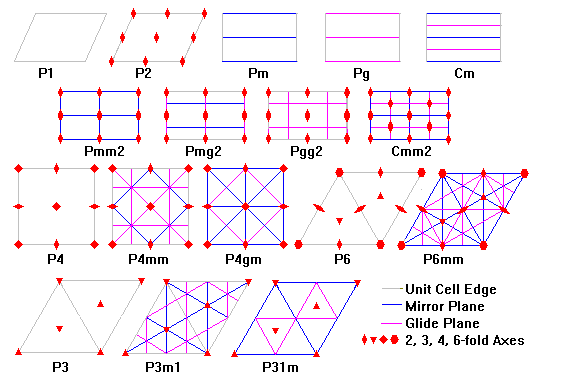

translations |

reflections |

reflections + |

glide |

reflections + |

rotations (2) |
reflections + |
rotations (2) + |

rotations (2) + |

rotations (4) |

reflections + |

rotations (4) + |

rotations (3) |

reflections + |

rotations (3) + |

rotations (6) |

reflections + |