Thursday February 2
More Puzzles and Polygons
- Tangrams. More
-
 Tangrams – Use
all seven Chinese puzzle pieces to make shapes
and solve problems.
Tangrams – Use
all seven Chinese puzzle pieces to make shapes
and solve problems. - Tangram Activity
Use templates to cut out pieces
from larger (blue) sheets. [#Partners=3.]
Geometric Puzzle Foundations
- Measuring angles, lengths and areas.
- Triangles
: add to 180 degrees- straight angle [Illustrate physically and with wingeometry]
- Squares, rectangles : 90 degree/ right
angle
- parallelograms: opposite angles are congruent,
sum of consecutive angles =180 degrees
- Dissections, cut and paste methods of measurement.
- Cutting and reassembling polygons.
- The
"Square Me" Puzzle
- The triangle, quadrilateral, pentagon, and hexagon.
More on measurements of angles of polygons with n sides. .
When n = 3 this is a triangle, n=4, a quadrilateral, or
when n= 5, a pentagon.
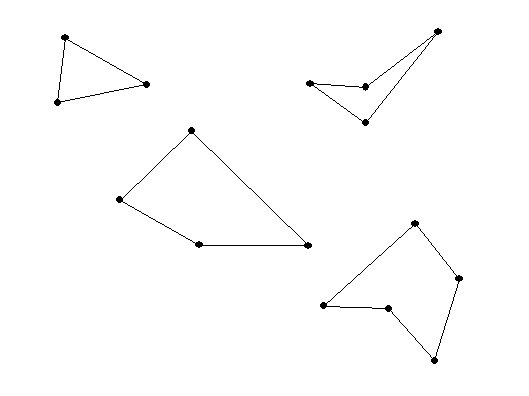
The sum of the measures of the
interior angles of a triangle is 180 degrees.
What about a quadrilateral? and a pentagon?
or an n sided polygon ( an "n -gon")?
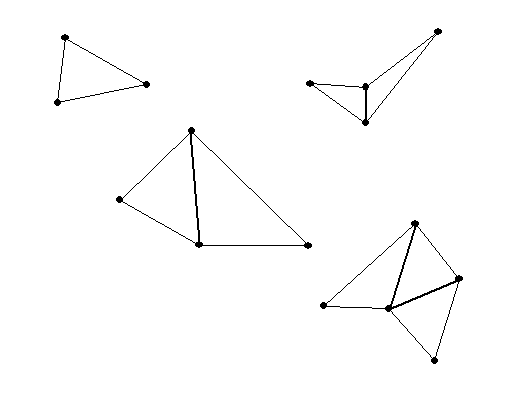
- A quadrilateral can be made from two triangles...
so the sum of its interior angles is 2 * 180 = 360.
- A pentagon can be made from 3 triangles...
so the sum of its interior angles is 3* 180 = 540. If the pentagon has
all angles congruent( of equal measurement) then each angle will be 540/5
= 108 degrees!
- A hexagon can be made from 4 triangles...
so the sum of its interior angles is 4* 180 = 720. If the hexagon has all
angles congruent( of equal measurement) then each angle will be 720/6 =
120 degrees!
From the figures we saw that for a quadrilateral (n =4), which can be dissected
into two triangles, the sum is 2*180= 360 degrees.
And for a pentagon (n=5)
which can be dissected into 3 triangles, the sum is 3*180=540 degrees.
# of sides
|
# of Triangles
|
Sum of Interior <‘s
|
If equal, Measure of a single <
|
3
|
1
|
180
|
60
|
4
|
2
|
360
|
90
|
5
|
3
|
540
|
108
|
6
|
4
|
720
|
120
|
N
|
?
|
|
|
In general: the sum
of the interior angles in a n sided polygon
is
(n-2) *180 degrees.
A regular polygon
is a polygon where the sides are all of equal length
and the angles are all congruent (or of equal measure).
Question: what is the measure of an individual
angle in a regular polygon with n sides?
For a triangle, the individual angle is 180/3
= 60 degrees.
For a square, the individual angle is 360/4=90
degrees.
For a regular pentagon.... 3*180/5 = 540/5
=108 degrees.
Now for a HEXAGON (6 sides) the sum of the angles
is 720 degrees.
So ... for a REGULAR HEXAGON,
the individual angle is 4*180/6 =720/6 =120 degrees.
In general: The individual
angle for a regular polygon with n sides is (n-2)*180/n degrees.
This can be expressed in other ways using algebra:
(n-2)*180/n = [180 n - 360] / n = 180 - 360/n.
| name of polygon |
|
degrees of the interior
measure of each angle |
360 degrees divided
by # in Column 2 |
| equilateral triangle |
3
|
60 |
360 / 3 = 120 |
| square |
4
|
90 |
360/4= 90
|
| regular pentagon |
5
|
3*180/5= 108
|
360/5= 72
|
| regular hexagon |
6
|
4*180/6=120
|
360/6= 60
|
| regular heptagon |
7
|
5*180/7
|
360/7
|
| regular octagon |
8
|
6*180/8=135
|
360/8 = 45
|
regular dodecagon
|
12
|
10*180/12=1800/12=150
|
360/12=30
|
Cutting and reassembling polygons.
Convex: Any two points in the figure
have a line segment connecting them. If that line segment is always inside the figure, then the figure
is called "convex".
Making Dissection Puzzles [more links] :
Dissection of the plane--- Tilings
of the plane:
Tessellations
- Activity: Tile plane with playing cards.
- FAPP watch Video: Possible tiles and tilings.
- One Regular Convex Polygon.
- Two or more Regular Convex Polygons.
- Other Polygon Tilings.
- Non polygonal tilings.
- One polygonal Tile: Quadrilateral Activity.
-
An on-line tool for making tilings of the plane
- Regular and semiregular Tilings of the plane. Some explorations - classification.
- A tiling is a regular tiling if (i)it has a single tile shape that
is a regular polygon and (ii) the vertices and edges of the tiles coincide
(no overlapping edges)
- A tiling is a semi-regular tiling if (ii) each tile shape is a regular
polygon, (ii) the vertices and edges of the tiles coincide (no overlapping
edges) and (iii) every vertex has the same polygon types arranged around
it.
- Wingeometry download!
and demonstrate tesselations.
- Naming tilings
(Math Forum)
- The numbers represent the number of sides in the poygons.
- The order indcates the order in which the poygons are arranged about
a vertex.
- Semiregular Tilings: global results!
Look at the results using wingeometry.
- Student lesson
(Math Forum) a place for further explorations on-line.
 Tangrams – Use
all seven Chinese puzzle pieces to make shapes
and solve problems.
Tangrams – Use
all seven Chinese puzzle pieces to make shapes
and solve problems.
 Tangrams – Use
all seven Chinese puzzle pieces to make shapes
and solve problems.
Tangrams – Use
all seven Chinese puzzle pieces to make shapes
and solve problems.

