-
The 13 Archimedean Solids
|
Spatial Symmetry
The Platonic and Archimedean Solids. |
- Translations
- Rotations: Center point - central axis
- Reflection : across line - across plane
- Rotations
- reflections
- rotation- reflection
| The 13 Archimedean
Solids |
|
Spatial Symmetry
The Platonic and Archimedean Solids. |
Topology
vocabulary:
"Bounded" In the plane- A line segment is bounded. A line is not bounded. A circle is bounded. A parabola is not bounded. "Bounded" means the object can be visualized in a box.
"closed" A line segment with endpoints is closed. A
circle is closed. A line is closed. A line segment missing one or
both endpoints in not closed. A circle missing one point is not closed.
"open" A line segment missing both endpoints is open.
A line is open. A
circle missing one point is open.
"connected" A line, a line segment, a circle, a circle missing
one point, and a parabola are all connected.
A line segment missing an interior point is not connected.
It has two pieces.
The following two letters
are closed, bounded, connected and topologically
equivalent.
The following two letters
are
topologically equivalent to each other but not to the previous two
letters. This can
be seen by removing a single point from these letters
which will not disconnect the curves, as it does with the previous
letters.
The letter T
missing the point where the top meets the vertical line segment is not
connected. It has three pieces.
The letter Y missing the point where the
top meets the vertical line segment also is not connected. It has three
pieces.
T and Y are topologically the same (equivalent)! this can be seen by bending the
tops to the letters up or down and stretching and shrinking the lengths
as
well.
Questions: Is a triangle topologically related to
another triangle?
Yes. Stretch the sides and you'll also transform the angles.
Is an circle topologically related to a line? No.
The circle is bounded and still connected when you remove a point.
The line is not bounded and is disconnected when you remove a point.
Is a triangle topologically related to a square?a circle? yes.
Topology and measurements:
Counting on a line. Counting
on a curve.
Keep count on the number of vertices and segments for a
graph. Compare:
| Vertices |
Edges |
V-E |
|
| Line
segment I |
2 |
1 |
1 |
| circle
O |
1 |
1 |
0 |
| 8 | 1 |
2 |
-1 |
| 9 | 2 |
2 |
0 |
| B | 2 |
3 |
-1 |
Curves will not be topologically
equivalent
if the number V-E is not the same.
However, as the table shows,
there are
curves that have the same number V-E which are also not equivalent.
These can be distinguished by other criterion, such as connectivity when a point is removed.
The number V-E is a
characteristic of the curve
that will be the same for any topologically equivalent curve.
However, this number does not completely classify the curves topologically, since curves can have the same number V-E without being equivalent.
Counting in the plane or Counting
on a surface.
Vertices, edges, regions.
| Vertices |
Regions | Edges | |
| Line segment | 2 |
1 |
1 |
| circle | 1 |
2 |
1 |
| 8 | 1 |
3 |
2 |
| 9 | 2 |
2 |
2 |
| B | 2 |
3 |
3 |
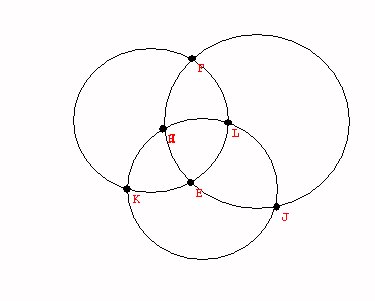
|
6 |
8 |
12 |
Counting in the plane or Counting on a sphere.
Euler's
Formula for the plane or the sphere:
Theorem: For any connected graph in the plane,
The number 2 is called the "Euler
characteristic for the plane." ( and the sphere).
Proof: Deconstruct
the graph.
First remove edges to "connect regions" until there is only one
region. The relation between V+R and E+ 2 stays the same.
(One edge goes with one region.)
Now remove one vertex and edge to "trim the tree".
Again the relation between V+R and E+2 stays the same. ( One edge goes
with each vertex.)
Finally we have just one vertex, no edges, and one region.
So the relationship is that V+R = E + 2!
For any connected graph on the sphere, V+R = E + 2
Proof:
Choose a point P on the sphere not on the
graph.
Place a plane touching the sphere opposite to P.
Then project the
graph onto the plane.
The projected graph will have the same number of vertices,
edges and regions.
The counting in the plane shows that the formula is true
for the projected graph, and thus for the original graph on the sphere!
What about graphs on the Torus?
We have a connected graph on the torus with one vertex, two edges and
only on region. But this information does not match for the euler
formula for the
plane or the sphere. SO.. the torus must be topologically different
from the
sphere or the plane!
In fact for the torus we see that it is possible for V+R= E or
V-E+R= 0
Summary: We have learned about
(and proved) Euler's
Formula
for the plane or the sphere: