Tuesday 11-8 and Thursday 11-11



Surfaces:Mark Sudduth's web page of surfaces.[ A physics master's degree student at UT, Arlington.]

    What is a surface?
    Bounded, unbounded:
    Closed, open:
    With or without boundary:
    Orientable or Non-orientable:
    Can be realized (imbedded) in a plane, in 3 space, in 4 space.
    Can be visualized (immersed) in ...

    Examples:A closed disc, an open disc, a plane, an annulus- cylinder, a mobius band;


 Mobius Strip

    Experiments with the mobius band. Activity.

    A sphere

    A torus


  Torus
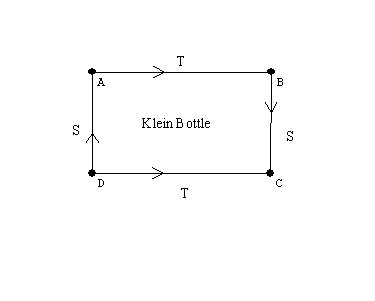
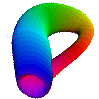
A Klein bottle:

Klein Bottle

  
An introduction to the fourth dimension:

A progression: Point and segment on a line, line segment and square in a plane (2-dim), square and a cube in space (3-dim), cube and a "hypercube" in hyperspace (4-dim)

The  Hypercube and coordinates:
What do we measure?  How does this determine "dimension?"
For a Line segment we can use one number to indicate distance and direction from a single point:  0 .... 1

For a Square we use two "coordinates" and we can identify the vertices of the square: (0,0), (1,0), (0,1),(1,1)

For a Cube  we use three "coordinates" and we can identify the vertices of the cube with qualities such as "left..right", "up... down", and "front ... back":
(0,0,0) , (1,0,0), (0,1,0),(1,1,0)
 (0,0,1), (1,0,1), (0,1,1), (1,1,1)

For a Hypercube....we use four "coordinates" and we can identify the vertices of the hypercube with qualities such as "left..right", "up... down", and "front ... back" and "inside... outside": (0,0,0,0) , (1,0,0,0), (0,1,0,0),(1,1,0,0)
 (0,0,1,0), (1,0,1,0), (0,1,1,0), (1,1,1,0)
(0,0,0,1) , (1,0,0,1), (0,1,0,1),(1,1,0,1)
 (0,0,1,1), (1,0,1,1), (0,1,1,1), (1,1,1,1)

Another four dimensional object:
The hyper simplex!
point
line segment
triangle
tetrahedron ("simplex")


Cards and the fourth dimension.

(clubs,diamonds,hearts,spades)
                            (1,1,1,1)        (0,0,0,0)
                             (1,1,0,1)        (0,0,1,0)
                             (0,1,0,1)        (1,0,1,0)
                             (0,0,0,1)        (1,1,1,0)
                             (0,0,0,0)        (1,1,1,1)

Hamiltonian Tour:  move through each vertex once and only once.

13 cards   : (5,3,0,5)   (4,2,6,1)

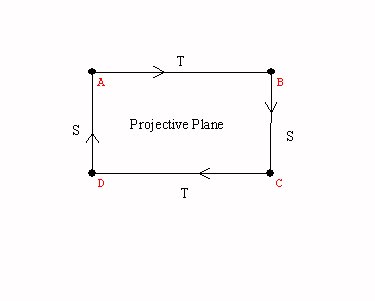
    The projective plane


 

    Spheres with handles:

Boy's Surface

    Spheres with cross caps

Crosscap .

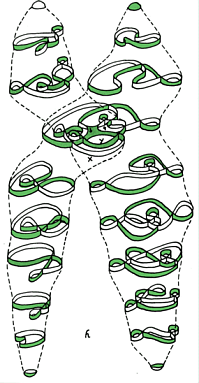
    Visualizations of surfaces by flattened - cut apart models.
    A cylinder, a mobius band, the torus, the Klein bottle, the projective plane.

    Handles and cross-caps  attached to the sphere.

Games and puzzles on the torus and the klein bottle.


" If Mathematicians Made Pretzels" Proof without words.
The following two figures are topologically equivalent.
From the Fun Fact files, hosted by the Harvey Mudd College Math Department , 

Unbelievable Unlinking

Figure 1
Figure 1
Figure 2
Figure 2

Imagine that the two objects in Figure 1 are solid (with thickness) and made of very flexible and stretchy rubber.

Question: is it possible to deform one object into the other in a continuous motion (without tearing or cutting)?

Surprise answer: Yes!!

Hint: it is important that the object is solid and has thickness; this transformation cannot be done with a one-dimensional piece of string. It is also not possible to do this with a piece of rope because even though the rope has thickness, it is not flexible or "stretchy" enough. See below for an explanation and animated gif. Or, don't scroll down if you want to think about it a while!

The Math Behind the Fact:
One way to do this is the following. Widen one of the loops and move one of its handles along the stem between the two loops to the other loop and push it through the hole so that the two loops become unlinked. The reference contains a sequence of pictures of this transformation.

Graeme McRae has generously contributed the animated gif in Figure 2, showing another solution to this problem! (Thank you, Graeme!)
Here is the original picture:

Ways to think of surfaces : cross-sections/ projections/moving curves/ using color to see another dimension.   ChromaDepthTM 3D;    CD Image gallery
3D image Gallery - click here!Tradtional  red/green 3D,

How do 3d glasses work? |
Spheres with handles,


    Visualizations of surfaces by flattened - cut apart models.
    A cylinder, a mobius band, the torus, the Klein bottle, the projective plane.

    Closed Surfaces: Handles and cross-caps  attached to the sphere.
Torus
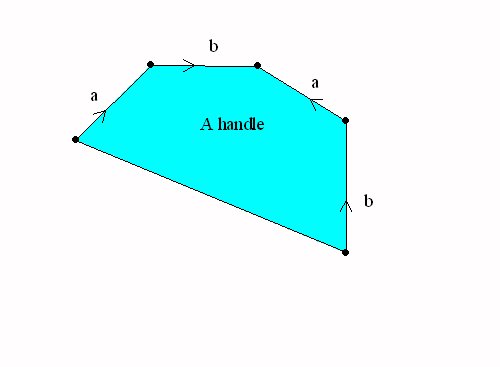
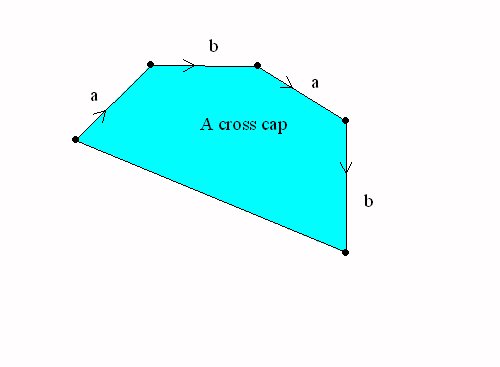
A sphere with a handle = a torus
 Crosscap
A Sphere with a cross cap = the projective plane


    The Topological Classification of "closed surfaces."

    Every connected closed and bounded surface is topologically equivalent to a sphere with handles and crosscaps attached.

    Proof....

Post proof remarks:
This classification determines the euler characteristic of each surface.
If the surface is orientable, it is a sphere with n handles, so V-E+R = 1 - 2n +1 = 2-2n.  For example the torus has euler characteristic 2-2*1=0.
If the surface is non-orientable, then  is it a sphere with k crosscaps and n handles, so the euler characteristic is V-E+R = 1 - (k+2n) +1 =2 -2n -k.
Notice that a sphere with two cross caps has euler characteristic 0, the same as the torus. But this was the euler characteristic of the Klein Bottle. So we should be able to recognize the Klein bottle as a sphere with two cross caps.
This can be done by a single normalization of one pair of edges with the same  orientation.
Other interest in surfaces: Examples
Ways to think of surfaces : cross-sections/ projections/moving curves/ using color to see another dimension.

Generalization of surfaces are called "manifolds".  cross sections / projections/ moving surfaces-solids.
"minimal surfaces" (FAPP video?)
Transforming surfaces: "turning the sphere inside out." video