Math 105
Thursday, November 17
"Seeing the Infinite"
Seeing
the infinite... small and large.
How many points are there on a line segment? Can you count them all?
Any list (possibly infinite) of points in a given segment of a euclidean
line will not have every point in that segment on the list.
Note that we can make a list of points corresponding to the rational
numbers once a unit length had been established.
1/1,2/1,3/1,4/1,...
1/2,2/2,3/2,...
1/3,2/3,...
1/4, ....
What is a
curve?
Curves and approximations of curves by line segments and polygons.
Regular Polygons and the circle.
The length of a curve.
Infinite curves: The snowflake.
Activity on snowflakes.
WinFeed (old version)
Space
filling curves.
How to see the
Infinite using "Projective geometry".
We will try to understand
- why we see the horizon on a plane....
- why the horizon is a
line composed of ideal/infinite
points.
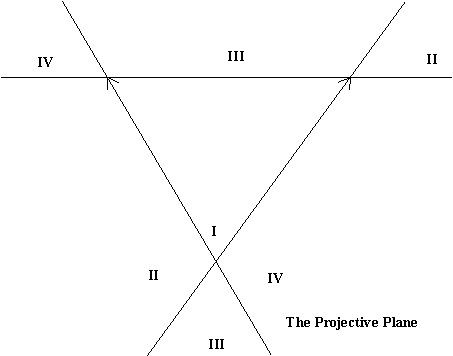
- why parallel lines "meet" on the horizon.
Center of projection/ perspective.
[compare with similarity and geometric series].
Correspondences:
Two Line segments of different length.
Semicircle to line and line to semicircle!
Two points at "infinity"
Circle to line and line to Circle!
One point at "infinity"
How to see the Infinite on a line using Projective geometry.
Line to Line
Use Rope and lines on floor with
an image plane to see parallels meet on an "image" plane ---
where is the horizon?
Perpective between planes in
Space!
Seeing the horizon on a plane.... a line of ideal/infinite points.
How parallel lines "meet" on the horizon.
What is the Affine Plane? the Projective Plane?
How do we see curves in perspective, drawn in the
Projective Plane?
Using coordinates to draw in perspective.
Creating coordinates in the affine plane.
Question: What is on the other side of the horizon?
Distinguish: The affine plane from the projective plane.
Using coordinates to transfer a circle to the affine plane as an ellipse.
Equations for conics in coordinate geometry.
Using coordinates to draw in perspective.
What do the conics look like in a perspective drawing or in the projective
plane?
Some final remarks on the projective plane
and visualizing Flatland and Space.:
- What is on the other side of the horizon?
- The projective plane as a surface.
- Visualizing the projective plane on a
disc with the boundary identified as the horizon.
- The projective plane as a non-euclidean
flatland.