Topology and measurements:
Counting on a line. Counting on
a curve.
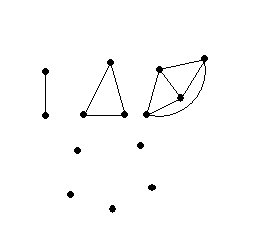
Keep count on the number of vertices and segments for a graph.
Compare:
| Vertices |
Edges |
V-E |
|
| Line
segment I |
2 |
1 |
1 |
| circle
O |
1 |
1 |
0 |
| 8 | 1 |
2 |
-1 |
| 9 | 2 |
2 |
0 |
| B | 2 |
3 |
-1 |
Curves will not be topologically equivalent
if the number V-E is not the same.
However, as the table shows, there are
curves that have the same number V-E which are also not equivalent.
These can be distinguished by other criterion, such as connectivity when a point is removed.
The number V-E is a characteristic
of the curve that will be the
same for any topologically equivalent curve.
However, this number does not completely classify the curves topologically, since curves can have the same number V-E without being equivalent.
Review from last class:
Counting in the plane or Counting on
a surface.
Vertices, edges, regions.
| Vertices |
Regions | Edges | |
| Line segment | 2 |
1 |
1 |
| circle | 1 |
2 |
1 |
| 8 | 1 |
3 |
2 |
| 9 | 2 |
2 |
2 |
| B | 2 |
3 |
3 |
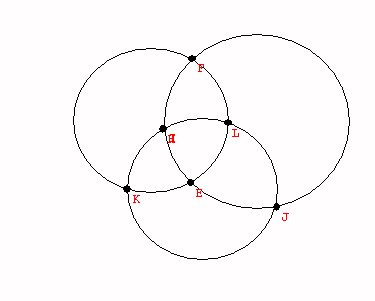
|
6 |
8 |
12 |
Counting in the plane or Counting on a sphere.
Euler's
Formula for the plane or the sphere:
Theorem: For any connected graph in the plane,
The number 2 is called the "Euler characteristic
for the plane." ( and the sphere).
The idea of the Proof:
Deconstruct the graph.
The relation between V+R and E+ 2 stays the same. .... [First to obtain
one region, then to obtain a single vertex... staying connected at all times!]
Finally we have just one vertex, no edges, and one region.
So the relationship is that V+R = E + 2!
For any connected graph on the sphere, V+R = E + 2
Proof:
Choose a point P on the sphere not on the graph.
Place a plane touching the sphere opposite to P.
Then project the graph onto the plane.
The projected graph will have the same number of vertices, edges and regions.
The counting in the plane shows that the formula is true for the projected
graph, and thus for the original graph on the sphere!
What about graphs on the Torus?
We have a connected graph on the torus with one vertex, two edges and
only on region. But this information does not match for the euler formula
for the plane or the sphere. SO.. the torus must be topologically different
from the sphere or the plane!
In fact for the torus we see that it is possible for V+R= E or
V-E+R= 0
Summary: We have learned about
(and proved) Euler's Formula
for the plane or the sphere: