Martin Flashman's Courses
MATH 418 Complex Analysis Spring 2015
MWF 11:00 SH 002
Class Notes and Summaries
Week 1:
1-21: The first day of class was introductory.
The focus of the course will be to understand complex numbers,
functions of complex numbers, and the derivative, integral and series
calculi for complex functions.
Math 418 covers the calculus of complex numbers and complex number valued
functions of one complex variable.
Key theorems we will examine will involve continuity,
differentiability, and integrability. The first coherent and
somewhat successful presentation of calculus for complex functions was by Cauchy in the
early 19th century- about 150 years after the works of Newton and
Leibniz.
We will use a working definition for what a real number is: a real
number is any number that can be represented as a possibly infinite
decimal (positive or negative) or that can be thought of a the
measure of a length of a line segment either to one side or the
other of a specified point on on a given line an a specific unit for
measurement.
Details of the syllabus will be discussed further on Friday.
1-23 [More details to follow.]
The organization of the course:
details like tests, homework, etc. as described in the main
course page.
In the discussion reference was made to Polya's :
How to Solve It...
Polya describes 4 Phases of Problem Solving
1. Understand the problem.
2. See connections to devise a plan.
3. Carry out the plan.
4. Look back. Reflect on the process and results.
It is the first phase that is usually not recognized as being
essential. there is usually more to understand than is apparent.
Also mentioned were other texts in Complex Analysis : See Moodle lists.
On Proofs:
- Daniel Solow's work was mentioned with on-line references on home page.
- How to Read and Do Proofs by D.Solow
- The Keys to Advanced Mathematics by D. Solow
- Polya's :
How to Solve It... available on line:
https://notendur.hi.is/hei2/teaching/Polya_HowToSolveIt.pdf
Start work on Complex Numbers:
Reading through class as start on how to: SOS 1.10 (?); 1,12; 1.53; 1.54; 1.55a; 1.56a.;1.59
Algebra and geometry problems from (i) SOS 1.53-1.74 (ii) Aben Chapter 2 (3?)
Week 2
1-26: Continue work on Complex Numbers.
Possible pr/exercises to do in class: SOS 1.10 (?); 1,12; 1.53; 1.54; 1.55a; 1.56a.;1.59
Algebra and geometry problems from (i) SOS 1.53-1.74 (ii) Aben Chapter 2 (3?)
Class Problem work notes from "secretary's report".:
1.72.
Find an equation for (a) a circle of radius 2 with center at (-3, 4),
(b) an ellipse with foci at (0, 2) and (0, -2) whose major axis has
length 10.
(a) Let $z=x+iy$. We have a radius of 2, center at (-3,4), or $-3+4i$
Cartesian form: $(x+3)^2+(y-4)^2=4$
But this doesn't really answer this question the way we want it to...
Complex form: if the center is at $-3+4i$, and we want $r=2$, we are
saying that the distance away from $z$ to $3+4i$ is $2$. Recall that modulus of
$z$, $|z|$ measures distance/length of vector.
So, the equation is $|z-(-3+4i)|=2$
(b) foci (0,2) and (0,-2) are $2i$ and $-2i$, respectively
Recall
from the definition of an ellipse that the total of the distances from the foci
to a point on the ellipse will be equal to the length of the major axis.
So, $|z-(-2i)|+|z-2i|=10$
Note:
$|z|$ is a function that takes a complex number to a real numbers and
is not one to one. (Two different z values will map to the same real
number.)
Look at technology for visualizing complex numbers:
Geogebra -
1-28: Continue foundational work on Complex Numbers.
Start on how to: SOS 1.7(a); 1.19; 1,12; 1.22;1.43; 1.44; 1.55a; 1.56a.;1.59
Algebra and geometry problems from (i) SOS 1.75-1.99 (ii) Aben Chapter 2 (3?)
CORRECTION/NOTE from discussion of 1-26 : $ |z|^2 = z \cdot \overline z$.where $\overline {a+bi} = a - bi$.
Notes from "secretary's report":
1.82 Show that $2+i = e^{i \arctan(\frac 12)}$
Solution: If
$ z = a+bi$, we know that $|z| = \sqrt {a^2 + b^2}$. Also, we know that $\theta =
\arctan(\frac ba)$. Lastly, we know $z = a+bi = |z|e^{i \theta}$. Hence $|z| =
\sqrt{2^2 + 1^2} = \sqrt(5); \theta = \arctan(\frac 12)$. Therefore $z = 2+i = \sqrt 5 e^{i \arctan(\frac 12)}$.
We also "proved" Euler's formula, $e^{i \theta} = \cos(\theta)+i \sin( \theta)$, by
using the taylor series expansion of all three terms.
Since all three
series are absolutely convergent, we can rearrange the left side in such
a
way that $e^{i \theta} = \sum_{n=0}^{\infty} \frac{(i
\theta)^n}{n!} = \sum_{k=0}^{\infty} \frac{(-1)^k
\theta^{2k}}{(2k)!} + \sum_{k=0}^{\infty} \frac{(-1)^k i
\theta^{2k+1}}{(2k+1)!} = \sum_{k=0}^{\infty} \frac{(-1)^k
\theta^{2k}}{(2k)!} +
i \sum_{k=0}^{\infty} \frac{(-1)^k \theta^{2k+1}}{(2k+1)!}
= \cos(
\theta)+i \sin( \theta)$.
1.97 a) Find the roots of $z^4+81 = 0$.
Solution:
Note if $z$ is a root of the equation then $z^4=-81 = 81 e^{\pi i}$.
Using Euler's formula with $z = re^{i \theta}$, we have $r^4 = 81$,
hence $r = 3$. Also using
$z^n
= r^n(cos( (n \theta ) +isin( (n \theta ))$ with $n = 4$ we use the periodicity of the sine and cosine to conclude that
$4\theta = \pi, 3\pi, 5\pi,7\pi$. Therefore by solving and plugging
the $\theta$
values back into the sine and cosine functions we obtain the roots
are $z =3(\pm \frac{\sqrt 2}2 \pm \frac {\sqrt 2}2 i )$.
1-30 Notes from "secretary's report".
1.88 a) Prove that $r_1e^{i \theta_1} + r_2e^{i \theta_2} = r_3e^{i \theta_3}$
where
$r_3= \sqrt{r_1^2+r_2^2+2r_1r_2cos( \theta_1 - \theta_2)} $
and $\theta_3= \arctan(\frac{r_1sin( \theta_1)+r_2sin(
\theta_2)}{r_1cos( \theta_1)+r_2cos( \theta_2}))$.
Solution: We
know that a complex number, $a+bi$ can be written in the form $
re^{i \theta}$ where $ r = \sqrt{a^2+b^2}$ and $\theta = |arctan (\frac ba)$. If
we give ourselves 2 arbitrary complex numbers, $z_1=a_1+b_1i $and $ z_2= a_2+b_2i$,
we can say that the sum of two complex numbers amounts to complex
number $z_3= a_1+b_1i +a_2+b_2i= (a_1+a_2) +i(b_1+b_2)$.
Calculating the radius for $z_3$, we have $r_3 = \sqrt{(a_1+a_2)^2 +(b_1+b_2)^2)}$.
Recognizing
the "dot product" of the vectors $<a_1,b_1>\cdot<a_2,b_2> =
a_1a_2+b_1b_2 $, We see that $a_1a_2+b_1b_2 = r_1r_2cos( \theta_1
- \theta_2)$, and so substituting
into our modulus for $z_3$, we have $r_3= \sqrt{r_1^2+r_2^2+2r_1r_2cos(
\theta_1 - \theta_2)} $ as desired.
To
show that $\theta_3= arctan(((r_1)sin( \theta_1)+(r_2)sin(
\theta_2))/((r_1)cos( \theta_1)+(r_2)cos( \theta_2)))$, we know that
imaginary part for $z_3$ is given by $r_1sin( \theta_1)+ r_2sin(
\theta_2)$.
The
real part of $z_3$ is given by the sum of $r_1cos( \theta_1)$ and
$r_2cos( \theta_2)$. Taking the arctangent of these two components yields the
desired answer, $\theta_3= \arctan(\frac{r_1sin( \theta_1)+r_2sin( \theta_2)}{r_1cos( \theta_1)+r_2cos( \theta_2}))$.
Later in the class, a student posed a question: what is the value of $i^i$? Turns out it’s a real number(no pun intended)!

Solution: We use the fact that $i = e^{i \frac {\pi}2}$
We consider $i^i$ by applying exponent rules and we have $i^i = {(e^{i \frac{\pi}2 }})^i =e^{i\cdot i\frac{\pi}2}$
so.... $i^i = e^{-\frac{\pi}2} \approx 0.2078$. This was verified using GeoGebra.
Week 3
2-2: Solving Polynomial Equations-The Rational Root Theorem works for complex with polynomials with integer coefficients:
Take the ratio of the factors of the first and last coefficients and
proceed by trial and error. Long division is require.
Problem
1.101: Find the roots of $p(z)=z^5-2z^4-z^3+6z-4$.
Solution: Using the rational
root test, the possible roots are ±1, ±2, ±4. Using substitution, we
know that $p(1)=p(2)=0$.
So $q(z)=(z-1)(z-2)=z^2-3z+2$. Now we divide $p(z)$ by $q(z)$ to get $r(z)=z^3+z^2-2$. Hence,
$r(z)∙q(z)=p(z)$, and we have to find the roots of $r(z)$, which are $1, -1+i$ and $-1-i$.
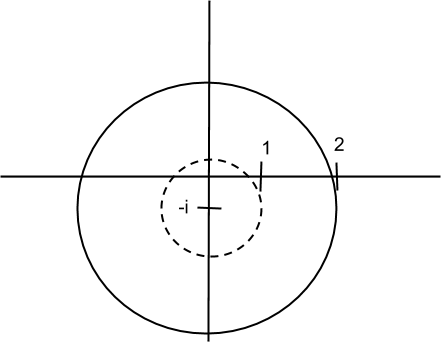
Region of complex inequality. In particular we looked at the “annulus” or “ring”.
$R_1<|z-(a+bi)|<R_2$ centered at $ a+bi$.
$1<|z+i|≤2$ is the region below in between the dashed-line circle and the solid-line circle.
2-4: Complex exponentials. $e^z=e^{x+iy}=e^xe^{iy}$.
Proving trigonometric identities using De Moivre’s theorem
Problem 1.93. Prove $\frac {\sin (4\theta)}{\sin (\theta)}= 8\cos^3(\theta) - 4 \cos(\theta) = 2\ cos(3\theta) + 2 \cos(\theta)$
Idea: $\sin(4|theta) = IM\{ ( \cos(\theta) + i \sin(\theta))^4\}$. This
turns out to have a common factor of $\sin(\theta)$.
2-6: Geometric interpretation of complex conjugate. $ z = x+ yi$ , $\overline z = x - yi$. $\overline z$ is denoted in the figure by $z^*$.
It's a reflection over the Real Axis
Problem 1.133. Let $P(z)$ be any polynomial with real coefficients. Prove $\overline {P(z)} =P( \overline z) assuming coefficients are real.
Idea: Use the facts that $\overline{z\cdot w} = \overline z \cdot
\overline w$, $\overline{z + w} = \overline z+\overline w$ and $\overline a =
a$ when $a$ is a real number.
Matrix interpretation of complex numbers
$1 : \left( \begin{array}{cc}1 & 0 \\ 0 & 1
\end{array} \right) \\ i : \left( \begin{array}{cc}0 & 1 \\-1
& 0 \end{array} \right)$
$a+bi = \left( \begin{array}{cc}
a & b \\
-b & a \end{array} \right) \\ |a +bi| = det \left( \begin{array}{cc}
a & b \\ -b & a \end{array} \right) $
Problem 2.50 (d) $f(z) =\frac{ z+2}{2z-1}$. Find values of $z$ such that $f(z) = z$.
Solution: $\frac{ z+2}{2z-1} = z$ so $z+2 = z \cdot (2z-1) = 2z^2 -z$.
So $2z^2 -2z -2 = 0$ or $z^2 -z -1 = 0$ and by the quadratic
formula $ z =\frac{ 1 \pm \sqrt{1 + 4 }}2 =\frac{ 1 \pm \sqrt 5}2 $. Checked with winplot:


Week 4
February 9th - 11th
On February 9th and early February 11th we worked on an example from the
text and studied some of the properties of the function provided using
the interactive complex mapping diagram.
The function we studied is as follows:
$f(z) = z(2 - z) = (x + iy)(2 - (x + iy))$ assuming $z = x + iy$
After smearing a little complex algebra around, we attained the real and
complex parts and expressed them as functions of $x$ and $y$ as
follows:
$f(z) = x(2 - x) + y^2 + i((2y - xy) - xy)$
which yields
$u(x,y) = 2x - x^2 + y^2$ and $v(x,y) = 2y - 2xy$
Surprisingly, the real and imaginary parts of $f(z)$ satisfy the
Cauchy-Riemman Condition which is a necessary condition for
differentiability of complex functions. Observe:
$\frac{\partial u}{\partial x} = 2 - 2x$
$\frac{\partial v}{\partial y} = 2 - 2x = \frac{\partial u}{\partial x}$
$\frac{\partial u}{\partial y} = 2y$
$\frac{\partial v}{\partial x} = -2y = -\frac{\partial u}{\partial y}$
You may study the function's properties using the complex mapping diagram found at:
We then looked at an example from the SOS pr/exercises where we showed the following:
All of the roots of $cos(z) = a$, where $-1 \leq a \leq 1$, are real.
Our immediate goal was to show that $Im\{ z \} = 0$.
This was done by expressing $cos(z)$ in terms of exponentials so:
Assume $cos(z) = a$, where $-1 \leq a \leq 1$. Then
$cos(z) = \frac{e^{iz} + e^{-iz}}{2}= a$
$\iff \frac{e^{iz} + e^{-iz}}{2} = a$
$\iff e^{iz} + e^{-iz} = 2a$
$\iff e^{iz} + \frac{1}{e^{iz}} = 2a$
$\iff(e^{iz})^2 + 1 = 2a e^{iz}$
$\iff(e^{iz})^2 - 2a(e^{iz}) + 1 = 0$
$\Rightarrow e^{iz} = a \pm \sqrt{a^2 -1}$
$\iff e^{-y}e^{ix} = a \pm i\sqrt{1 - a^2}$ assuming $z = x + iy$
$\Rightarrow|e^{-y}e^{ix}| = \sqrt{a^2 + 1 - a^2}$
$\iff e^{-y} = \sqrt1 = 1$ which happens only when $y = 0$
Thus $Im\{ z \} = 0$, and $z = x$, a real number.
Thus all of the roots of $cos(z) = a$, where $-1 \leq a \leq 1$, are real.
We ended lecture on Wednesday studying the geometric properties of basic functions on the $W$ - plane.
Using Winplot we looked at the most basic function:
$w = f(z) = z +a + ib $
Animating on $a$ and keeping $b$ constant makes the image of any point
on the $z$ - plane shift either left or right depending on the sign of
$a$. Similarly, animating on $b$ and keeping $a$ constant makes the
image of any point on the $z$ - plane shift either up or down depending
on the sign of $b$.
We next looked at the function:
$w = f(z) = z \cdot (a + ib)= z \cdot\rho e^{\theta i}$
Animating on $\rho$ "magnifies" the image of a set of points on the $z$ -
plane, while animating on $\theta$ rotates the image of a set of points
on the $z$ - plane depending on the angle $\theta$ of $(a + ib)$.
2-13
Example for HW Problem 2.83:
$f(z) = z^3 = (x+iy)^3 = x^3+3x^2iy+3x(iy)^2+(iy)^3 = x^3-3xy^2+(3x^2y-y^3)i$
$u(x,y) = x^3-3xy^2$
$v(x,y) = 3x^2y-y^3$
$\frac{du}{dx} = 3x^2-3y^2$
$\frac{du}{dy} = -6xy$
$\frac{dv}{dx} = 6xy$
$\frac{dv}{dy} = 3x^2-3y^2$
Note that $\frac{du}{dy}$ and $\frac{dv}{dx}$ are of opposite sign, but this is not always the case.
F$(z) = z = x-iy$
$\frac{du}{dx} = 1$
$\frac{du}{dy} = 0$
$\frac{dv}{dx} = 0$
$\frac{dv}{dy} = -1$
We then discussed the
general way that a derivative is found with linear functions, and how
this relates to finding derivatives of complex functions.
Linear function example for a real valued function:
$f(2) = 5$, $f(3) = 7$
What's the slope?
$\frac{f(3)-f(2)}{3-2} = \frac{7-5}{1} = 2$
$f(x) = 7+2(x-3) = 7+2x-6 = 2x+1$
Complex linear function example:
$f(1+i) = 2+i$, $f(1-i) = 1+i$
"Slope": $\frac{f(1+i)-f(1-i)}{(1+i)-(1-i)} = \frac{(2+i)-(1+i)}{1+i-1+i} = \frac{1}{2i} = \frac{-1}{2}i$
$f(z) = (2+i)+ \frac{-1}{2}i(z-(1+i)) = 2+i-\frac{1}{2}iz+\frac{1}{2}i-\frac{1}{2} = \frac{3}{2}+\frac{3}{2}i-\frac{1}{2}iz$
Check: $f(1-i) = 2+i+\frac{-1}{2}i(1-i-1-i) = 2+i-\frac{1}{2}i(-2i) = 2+i-1 = 1+i$
The term $\frac{-1}{2}iz$ serves as the rotation
factor. Any vector z is first cut in half and rotated 90 degrees
clockwise around the point $2+i$.
We then went to
An example: Using the definition of complex number derivatives for the function $f(z) = z^3$,
find $f'(z)$ when $z = 1+i$
Step 1: Evaluate
$f(z) = z^3$
$f(1+i) = (1+i)^3$
$f(1+i)$ has a length of $\sqrt{2}$ and angle
$\frac{\pi}{4}$, while $(1+i)^3$ has length $\sqrt{2^3}$ and angle
$\frac{3\pi}{4}$.
Step 2: Find the difference of the function values at $z$ and $1+i$.
$f(z)-f(1+i) = z^3-(1+i)^3$
Step 3: Divide:
$\frac{f(z)-f(1+i)}{z-(1+i)} = \frac{z^3-(1+i)^3}{z-(1+i)} = z^2+z(1+i)+(1+i)^2$, where $z \neq (1+i)$.
This solution holds from the rule of factoring cubic
polynomials for real number polynomials, since this rule works the same
for complex number polynomials
This is because the complex numbers and the real numbers are both "fields"..
Step 4: Think
Think about $z$ approaching $1+i$
As $z \to 1+i$ , we see that
$\frac{f(z)-f(1+i)}{z-(1+i)}= z^2+z(1+i)+(1+i)^2 \to 3(1+i)^2 = f'(1+i)$
There are two equivalent ways to define the complex derivative of
$w=f(z)$ at $z=z_0$, denoted $f'(z_0)$ or $\frac {dw}{dz}|_{z=z_0}$:
1: $\lim_{z → z_0} \frac{f(z)-f(z_0)}{z-z_0} = f'(z_0)$
2: $z-z_0 = \Delta z, \lim_{\Delta z \to 0} \frac{f(z_0+\Delta z)-f(z_0)}{\Delta z} = f'(z_0)$
Week 5
Notes: 2/16/2015 and 2/18/2015
Suppose $f(z)=u(x,y)+iv(x,y)$
$lim_{∆z →0}\frac{f(z+ ∆z)-f(z)}{∆z}$ ; Assumption: $f(z)$ has a derivative at $z$.
Assume $∆y=0$ then: $lim_{∆x→0}\frac{u(x+ ∆x,y)+iv(x+ ∆x,y)-u(x,y)-iv(x,y)}{∆x}$
$= ∂u/∂x+i ∂v/∂x$
Assume $∆x=0$: $lim_{∆y→0}\frac{u(x,y+ ∆y)+iv(x,y+ ∆y)-u(x,y)-iv(x,y)}{i∆y}$
$ = 1/i(∂u/∂y+i ∂v/∂y)$
$= (i/i)(1/i)(∂u/∂y+i ∂v/∂y)$
$= ∂v/∂y-i ∂u/∂y$.
Equate the real and imaginary components and we have the Cauchy-Riemann Equations!
$∂u/∂x= ∂v/∂y , ∂u/∂y= -∂v/∂x$
Example: $f(z)= 3z$,when $z\ne1$
$f(z)= 7$, when $z=1$.
Limits: we don’t care what actually happens at the point $z_0,$ only when near to $z_0$.
Notation: $D_δ={ z∶0< |z-1|< δ}$
Goal: be close to the target number
Find a way to describe $f(z)$ being close to $3$
Example: How do we make $f(z)$ Within $0.1$ of $3$.
|$f(z)- 3|< 0.1$
Find a set of $z$'s in the domain that satisfies closeness to $1$ ($\ne 1$)
We want $|3z- 3|< 0.1$.
or $|3(z- 1)|< 0.1$
that is, $3|z- 1|< 0.1$
so we want$ z-1|<\frac{0.1}3 ≈.03333333333333333333…$
Choose $\delta = 0.03$
Then if $0<|z- 1|< \delta$, then $f(z) – 3 = 3(z-1)$
So $|f(z)- 3|=3|z- 1|<3\delta = 0.09< 0.1$.
If you wanted to be within $0.01$ of $3$, I can find a deleted neighborhood of 1 with $\delta = 0.003$ where
if $0<|z- 1|< \delta$, then $f(z) – 3 = 3(z-1)$
So $|f(z)- 3|=3|z- 1|<3\delta = 0.009< 0.01$.
What about a tiny $\epsilon >0$?
Find a way to describe $f(z)$ being close to $3$ within $ε$ of $3$.
Given any $ε>0$-- so ...
Choose any $ε*>0$ (a fixed, specific $\epsilon$.)
Let $\delta = \frac{ε*}3$.
Then consider $z$ where $0< |z- 1|< \delta$.
Then $f(z) = 3z$
$f(z) – 3 = 3z – 3$
$ = 3(z-1)$
and sp $|f(z)- 3|=3|z- 1|<3\delta = 3 \cdot \frac{\epsilon *}3< \epsilon *$.
So $\lim_{z \to 1}f(z)= 3$.
2-20 SOS: Problem 2.89 (a) Show $lim_{z \to i} z^2+2z = 2i-1$.
Solution: Suppose $ \epsilon >0$.
We need to find $\delta >0$ so that
if $0<|z-i|<\delta$ then $|z^2+2z -(2i-1)| <\epsilon$.
Note that $|z^2+2z -(2i-1)| = |z^2- i^2 +2z -2i| = |(z+i)(z-i) +2 (z-i)| =|z+i+2||z-i|< |z+i+2| \delta$.
Since we can choose $\delta<1$ ,
we can show using the triangle inequality that $|z+i+2|=|z-i+2i+2| \le
|z-i|+|2i+2| <\delta + 3<4$. So $|z^2+2z -(2i-1)| < 4\delta$.
So we want $ \delta$ so that $4\delta < \epsilon$.
So choose $\delta = min\{ \epsilon/4 ,1/2\}$, and we have
$|z^2+2z -(2i-1)|< 4\delta \le 4 \epsilon/4 = \epsilon$.
Check with some GeoGebra examples on http://web.geogebra.org/app/?id=TBwX2yZs
Other discussion:
Consider $f(z) = \frac 1{z-i}$ and the definition of a "domain" for the
complex plane as an open and connected set of complex numbers.
The conventional domain of this function would be $D = \{z : z \ne i\}$
A set $O$ is defined as "open" if and only if for any $z_0 \in O$ there is a $delta \gt 0$ where$\{z:|z- z_0| \lt \delta \} \subset O$
With this definition one can show that $D$ is an open set.
Outline: Choose $z_0 \in D$. let $\delta = \frac{|z_0 -i|}2$. Then it
can be shown that $i \notin \{z:|z- z_0| \lt \delta \}$ we have $\{z:|z-
z_0| \lt \delta \} \subset D$ which shows $D$ is an open set.
For the concept of connected we can use a provisional definition that an open set $O$ is connected if given any two numbers in $O$, $w_1$ and $zw2$, there is a set of line segments in $O$ that "connect" the two numbers.
It was illustrated how the set $D$ is connected.
Proposition: If $S = \{ z_1, z_2, ...z_n\}$ is a finite set of complex numbers then $D = C - S$ is an open connected set.
Proof Plan: For $z_0 \in D$ let $\delta = \frac 12 \min \{|z_0-z_k|, k = 1, ... ,n\}$.
For any two numbers in $D$, $w_1$ and $w_2$ ,there is a set of line
segments that "connect" the two numbers while avoiding $S$, so the
segments are in $D$.
Final example: The set $S = \{z : z \ne \frac ik, k = 1,2,3,...\}$ is not an open set.
Discussion: Consider $z=0 \in S$. For any $\delta \gt 0$ there is a
number $k* \gt \frac 1{ \delta}$ so $|\frac ik | = \frac 1k \lt
\delta$ and thus there is no $\delta \gt 0$ where $\{z:|z-0| \lt \delta
\} \subset S$.
Week 6
Topology/Geometry of the Domain 
Definitions
Open Sets: A set $O$ is open if (and only if)
for all $z_0 \in O$, there is a number $\delta > 0$ so that
$\{ z :| z - z_0| < \delta \}\subset O$.
Closed Sets: A set $S$ is closed
if the complementary set $S^c = \{z : z \notin S \}$ is an
open set. In
other words: The set $S$ is closed if for any $z_0 \notin
S$, there is a number $\delta > 0$ so that $\{ z :| z - z_0|
< \delta \}\subset S^c$. Stated in a direct way: $S$ is a closed set
if (and only if) whenever $z_0 \in S$ and $\delta > 0$
either $\{ z :| z - z_0| < \delta \}\subset S $ or for any number
$\delta > 0$ , $\{ z :| z - z_0| < \delta \}$ contains an
element $z_* \in S$ and
$z' \notin S$.
Connected Sets. An open set S is said to be connected if any two
points of the set can be joined by a path consisting of straight line
segments (i.e., a polygonal path) all points of which are in S. 
Bounded Sets: The magnitude of all elements of a bounded set are smaller or larger than some given number.  Geometrically:
Geometrically:
Boundaries: The boundary of a set, $S$, denoted $\partial S$ is
given by those points which are surrounded by both points within and
outside of the set, that is, $z_0 \in \partial S$
if and only if for any number $\delta > 0$ , $\{ z :| z - z_0|
< \delta \}$ contains an element $z_* \in S$ and $z' \notin
S$.
Compact Set: A compact set is a set that is both closed and bounded.
Functions
2 main types of functions:
● Linear; of the form $f(z) = az + b$ where $a,b ϵ C $
● Mobius transformation; of the form $f(z) =\frac {az+b}{cz+d}$ where $a,b,c,d ϵ C$.
Functions transform the complex $z$ plane to the complex $w$ plane, where $w = f(z)$.
Three main notions about functions: Limits, Continuity, and Differentiability
Limits
The number $L$ is the limit of $f(z)$ as $z$ approaches $z_0$, written
as $\lim_{z→z_0} f(z) = L$, if for some small positive number $\epsilon
\gt 0$ we can find some small positive number $\delta \gt 0$ such
that $|𝑓(𝑧)−𝐿 |<\epsilon$ whenever $0 < |𝑧−𝑧_0| \lt
\delta$..
The limit must be independent of the manner in which $z$ approaches $z_0$.
Continuity
A function is said to be continuous at $z_0$ if $\lim_{z→z_0}f(z) = f(z_0)$. This implies the following three conditions:
1. $lim_{z→z_0} f(z) = L$ must exist
2. $f(z_0)$ must exist
3. $L = f(z_0)$.
Derivatives
The derivative of a single valued function, $f(z)$, in some domain of the complex $z$ plane is defined by:
$𝑓′(𝑧) = 𝑙𝑖𝑚_{\Delta z→0}]\frac { 𝑓(𝑧+𝛥𝑧)−𝑓(𝑧)}{ 𝛥𝑧 } $
provided that the limit exists independent of the manner in which $∆z$
goes to $0$. $f$ is said to be differentiable at $z$ if this is the
case.
A necessary condition for $f(z)$ to be differentiable at all points in a region is to satisfy the Cauchy-Riemann equations:
$\frac {\partial u}{\partial x} = \frac {\partial
v}{\partial y}$ and $\frac {\partial u}{\partial y} = -\frac {\partial
v}{\partial x}$
where $u$ and $v$ are respectively the real and imaginary parts of the transformation $f(z)$.
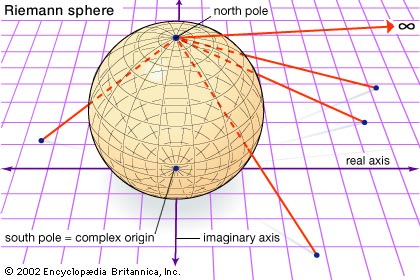
The Real Projective Line: 
Every point on the real number line gets associated with a point on a
unit circle. -infinity and +infinity get mapped to the “north” pole of
the circle which is refer as to the point at infinity. Visually:

The analog of the Cartesian plane for the Real Projective line is the torus.
A similar construction attaches a single point at infinity to the complex numbers creating the "Riemann sphere."
2-27
Compactness in the Complex plane.
Definition: A subset $K$ of the complex numbers is called compact if $K$ is closed and bounded.
Theorem : Heine- Borel. (Not proven here- see a real analysis or advance calculus course, e.g Calculus on Manifolds by M. Spivak.)
$K$ is a compact set if and only if for any family of open sets $\{U_{\alpha}\}$ with $\alpha \in I$, $ I$ an indexing set for the family of sets, with the property that $K \subset \bigcup U_{\alpha} $.
then there is a finite collection of the $
U_{\alpha}$, which we can denote $\{ U_1, U_2, U_3, ..., U_n\}$ where
$K \subset \bigcup U_j $.
Compactness and continuous functions.
Theorem: Suppose $f$ is a continuous function on a domain $D$ and $K$ is a compact subset of $D$. Let $K' = f(K)$. Then $K'$ is compact.
Proof: Basic outline using the topological characterization of compact related to open covers.
Suppose $U'_{\alpha}$ is a family of open sets with $\alpha \in I$, $ I$
an indexing set for the family of sets, where $K' \subset \bigcup
U'_{\alpha}$.
Let $U_{\alpha}= f^{-1}(U'_{\alpha})$.
Since $f$ is a continuous function, each $U_{\alpha}$ is an open set and $K \subset \bigcup U_{\alpha}$.
Now since $K$ is compact, there is a finite collection of the $
U_{\alpha}$, which we can denote $\{ U_1, U_2, U_3, ..., U_n\}$ where $K
\subset \bigcup U_j$.
Now consider the corresponding family of sets, $\{ U'_1, U'_2, U'_3, ..., U'_n\}$.
For any $w' \in K'$, $w' = f(z)$ for some $z \in K$. But we have $z \in
U_j$ for some $j$, so $w' = f(z) \in U'_j$. Thus if $w' \in K' = f(K)$,
then $w' \in \bigcup U_j '$, so $K' \subset \bigcup U'_j$ for a finite
number of the original $U'_{\alpha}$. Thus $K'$ has been shown to be
compact. EOP.