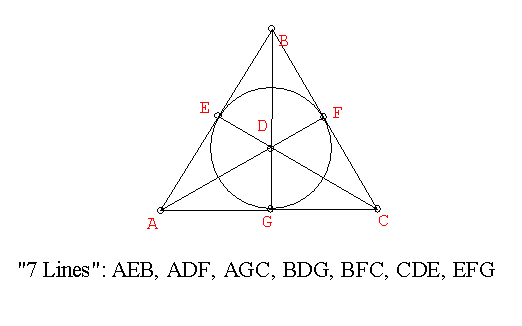
Connecting Axioms to Models.
We can visualize the seven point- seven line geometry
using the following figure:
-
It is apparent from this figure that 7 points are enough
to satisfy the axioms for the seven point geometric structure described
in
the reference, and that any more points would force a violation of
one of the axioms.
You should work through this argument yourself. Suppose there is an eighth point, H.
Then there must be an eighth line determined by A and H. [why?]
But can AH have a point in common with the line with points BCF?
No... can you see why having a point in common with BCF would be contrary to the axioms. Which axioms would be violated?
In a geometry structure we use a language with words
like "point" and "line" for objects and relations between these objects
like "is on" or "passes through" and operations on these objects
like "meet", "intersect" and "join".
In the structure initially we list certain properties
(axioms) of the objects that are supposed as "true", and we use logic to
infer (deduce) other properties (theorems) of the objects.
A (set theoretic) interpretation for a geometry structure
is a set in which the words of the geometry stucture's language are identified
with set elements and sets and relations and operations on sets.
If any
(and every) true statement (theorem) about the mathematical structure is also true
of the corresponding statement about the interpretation, then the
interpretation is called a model for the geometric structure.
Thus we can say that an interpretation for the geometric
structure described previously with point and lines is given by a set of
objects labelled A,B,C,D,E,F, and G.
Points correspond to the objects.
Lines correspond to sets of three objects from one of the seven previously
described sets: {A,E,B}, {A,D,F}... {E,F,G} .
A point is on a line
if the object is an element of the line set.
This interpretation is a model
and it is visualized by the previous "7 line" triangular figure.
Another interpretation for a geometric structure might
involve just 3 objects, A,B and C, for points and three lines {A,B}, {A,C},
and {B,C}.
This might be represented by the three vertices of a triangle.
This geometry does not satisfy the first axiom for
the previously described geometric structure, because a line does not have
three distinct points.
It does satisfy the other three axioms. So
this interpretation is not a model for that structure!
However, there is something to be learned about that
structure from the two interpretations we have discussed.
From the first model with the 7 points and 7 lines we can see that the axioms
for the structure are consistent in the sense that it is not possible to
derive a logical contradiction from these axioms. [If such a contradiction
could be logically inferred, then the model would have to exhibit this contradiction!]
From the second model with the 3 points and 3 lines we can see that a collection
of axioms based on the negation of the first axiom but otherwise the same
as the axioms for the geometric structure are also consistent.
Since both the first axiom and it negation appear to be consistent with the
other axioms, it is not possible to infer the first axiom or its negation
from the other axioms.
Thus the existence of the two different models allows us to infer that the
first axiom (and it's negation) cannot be logically inferred from the
other axioms, i.e., the first axiom is independent of the other axioms.