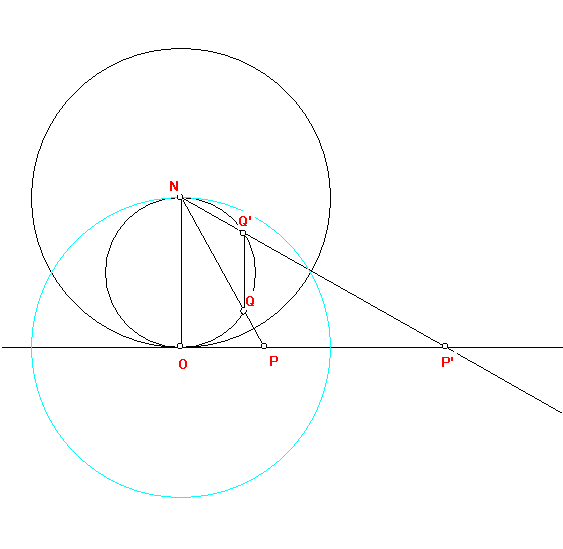
Suppose P is on l and PN intersect C = {Q}; Q' is on C so that Q'Q is parallel to ON; and {P'} = NQ' intersect l.
TEXTS: Fundamentals of Geometry by B. Meserve and J. Izzo,
A.W. (1969) -
ON LINE
through Moodle.
The
Elements by Euclid, 3 volumes, edited by T.L. Heath, Dover
(1926)
Proof in Geometry by A.I Fetisov, Mir (1978)
Flatland By E. Abbott, Dover.
| Week | Monday | Wednesday | Friday | Reading/Videos for the week. | Problems
Due on Wednesday of the next week |
|---|---|---|---|---|---|
| 1 | No Class |
1-21-09 1.1 Beginnings |
1-23 |
M&I:1.1,
1.2
E:I Def'ns, etc. p153-5; Prop. 1-12,22,23,47 A:.Complete in three weeks |
Due:1-30-09 M&I p5:1-8,11 |
| 2 | 1-26 The Pythagorean Theorem
|
More on Pythagoras and Euclid. |
1-30 Prop 2 Begin disssection theory, |
M&I
1.2, 1.3
E: I Prop. 16, 27-32, 35-45. |
Due: 2-4 M&I: p10:1,2,5,10,11-13 Prove:The line segment connecting the midpoints of two sides of a triangle is parallel to the third side and is congruent to one half of the third side. [ HELP! Proof outline for the midpoint proposition.] |
| 3 | 2/2Convexity defined. Equidecomposable Polygons Constructions Isometries 1.1 Def'ns- Objects | 2/4 1.2 Constructions 1.4 Continuity | 2/6 1.3 Geometry: Constructions and numbers | M&I
1.3,1.4
E: III Prop. 1-3, 14-18, 20, 21, 10 Here’s looking at Euclid F. Sect. 11, 25, 31 Watch Equidecomposable Polygons | Due: 2-13 (changed 2-13!) M&I: p11: 16-19, 24, *27 Problem Set 1 |
| 4 | 2/9 More on continuity and rational points. |
2/11 Start Inversion Orthogonal Circles |
2/13More on Cantor Similar triangles Odds and ends. Coordinates. |
M&I:1.5,
1.6,
2.1
E: V def'ns 1-7;VI: prop 1&2 F. Sect. 32 |
Due 2-18 M&I: p17: 5, 8-11 p23: 9,10 (analytic proofs) |
| 5 | 2/16 Odds and ends | 2/18 Odds and ends |
2/20Start: Transformations - Isometries Transformations - Isometries. |
M&I:
2.1, 2.2
E: V def'ns 1-7;VI: prop 1&2 E:IV Prop. 3-5 Isometries (Video # 2576 in Library) . |
Due: 2-25 M&I:1.6:1-12,17,18 Problem Set 2 |
| 6 | 2/23More Isometries: Coordinates and Transformations classification |
2/25 More on Isometries |
2/27 .... |
M&I: 2.1,2.2 | Due 3-4 Problem Set 3 (Isos Tri) [3 Points for every distinct correct proof of any of these problems.] |
| 7 |
3/2Finish Classification of Planar Isometries. Begin Affine Geometry |
3/4
Isometries and symmetries |
3/6
Proportion and Similarity |
M&I: 2.2 again;3.1,3.2, 3.5 | Quiz #1 on 3/11 See Sample quiz on Moodle. |
| 8 |
3/9 More on Similarity |
3/11 Inversion and Affine Geometry (planar coordinates) the Affine Line. | 3/13 Constuctions with Straight edge and compass. | M&I:3.6,
3.4,3.7 View video (in Library #4376 ) on "Central similarities" from the Geometry Film Series. (10 minutes) View video (in Library #209 cass.2) on similarity (How big is too big? "scale and form") "On Size and Shape" from the For All Practical Purposes Series. (about 30 minutes) |
|
| 9 Spring break | 3/16 No Class |
3/18 No Class | 3/20 No Class | ||
| 10 | 3/23 Visualizing
the affine plane. Seeing the infinite.Affine geometry- Homogeneous coordinates and visualizing
the affine plane. |
3/25 More on Homogeneous coordinates for the plane.A first look at a "Projective plane." Axioms, consistency, completeness and models. |
3/27Begin Synthetic Geometry [Finite] Algebraic-projective geometry: Points and lines. Spatial and Planar Axioms for 7 point geometry. Begin Synthetic Projective Geometry |
A non-euclidean universe. M&I :3.1, 3.2, 3.5, 3.6, 3.7; 4.1 |
Due : 4/1 M&I: 3.5: 1,3,4,5,10,11 3.6: 3,7-15 3.7: 1,4,7,10,13 |
| 11 | 3/30 Homogeneous Coordinates with Z2 and Z3 More on Finite Synthetic Geometry and models. Proof of Desargues' Theorem |
4/1 -Projective Geometry -Visual/algebraic and Synthetic..Axioms 1-6 Projective Planes. . | 4/3. More on the axioms of Projective Geometry.RP(2) as a model for synthetic geometry. |
M&I:4.1, 4.2, 4.3, 2.4 | |
| 12 | 4/6 Proofs of some basic projective geometric facts. | 4/8
Triangle Coincidences (Perpendicular Bisectors- the circumcenter) Applications of Projective Geometry Postulates.1-6 |
4/10 Quiz #2 Desargue's Theorem and Duality |
Due 4/15 M&I: 4.1:7,15,16; Prove P6 for RP(2); 4.2: 2,3, Supp:1 4.3: 1-6, Supp:1,5,6 |
|
| 13 | 4/13 Conic Sections.
More Duality |
4/15 More Postulates- Sections (more duality) Complete quadrangles Postulate 9. |
4/17 Perspectivities and Projectivities. Projective transformations. Conics Pascal's Theorem ? More on coordinates and transformations. |
M&I:
4.5,4.6(p94-97).4.7, p105-108 (Desargues' Thrm) Watch video: "Conics" [VIDEO #628]. Watch video: For All Practical Purposes on conicsFAPP on conics[HSU Video #209- 3. Stand-up conic (Conic sections) (ca. 30 min.)]. WatchVideo: Orthogonal Projection [Video #4223] |
Due : 4/22 Problem Set 4 |
| 14 | 4/20Projectivities. Perspective | 4/22Transformations of lines with homogeneous coordinates | 4/24 Projectivities in 3 space: More on Projective Line Transformations with Coordinates. Begin Harmonic Sets and Construction of Coordinates. | 4.10, 5.4, 2.4
4.11 |
Due: 4/29 M&I: 4.5:2 ;4.6: 7,8,9; 4.7: 4,7 4.10: 4,5,9,10 [Prove P9 for RP(2),optional] |
| 15 Final exam available 4/30. |
4/27Harmonic sets: uniqueness and construction of coordinates for a Projective
Line, Plane, Space. |
4/29More on Transformations, Coordinates and Harmonic sets. | 5/1 | 5.1,5.4;,5.2, 5.3,5.5, 5.7, 6.1, 6.2 | |
|
16 Final projects are due for review Tuesday, May 5th. |
5/4
Projective generation of conics Pascal's and Brianchon's Theorem. |
5/6 Matrices for familiar Planar Projective Transformations. Inversion angles, circles and lines? |
5/8 The Big picture in Summary. |
|
|
| |
|
|
|||
|
|
|
Due: M&I: 4.10:1,3,6,7; 5.4:1-8,10; 5.5: 2,3,7 |
|||
|
|
Due: M&I: 4.10:1,3,6,7; 5.1:5; 5.4:1-8,10; 5.5: 2,3,7 |
||||
| 16 |
Conics revisited. Inversion and the final exam. Quiz #3 |
|
. Student Presentations |
A Project Fair will be organized for displays and presentations during the last day of class. Details will be discussed later.
Guidelines for Preliminary Proposals:
| Tiling patterns - tesselation 3d tiling MC Escher perspective Curves: conics, etc. optical illusions knots fractals Origami Kaleidescope Symmetry The coloring problem Patterns in dance and other performance arts Flatland sequel (4d) | Maps Juggling structural Rigidity dimension Polyhedra bridgemaking (architecture) Models (3d puzzles) paper mache or clay mobiles sculpture A play - movie build three dimensional shapes power point performance website |
DEFINITIONS: A figure C is called convex if for any two
points in the figure, the line segment determined by those two points is
also contained in the figure.
That is, if A is a point of C and B is a point of C then the line segment
AB is a subset of C.
If F and G are figures then F int G is { X : X in F and
X in G }.
F int G is called the intersection of F and G.
If A is a family of figures (possibly infinite), then int
A
= { X : for every figure F in the family A, X is in F }.
int A is called the intersection of the family A.
-----------------------------------------------------------------
1. Prove: If F and G are convex figures , then F int G is a convex figure.
2. Give a counterexample for the converse of problem 1.
3. Prove: If A is a family of convex figures, then int A is a convex figure.
4. Prove: The line segment RS is convex. [ Refer to M & I pg.2.]
1. Suppose n is a natural number. Given P0 and P1 , prove by induction that you can construct with straight edge and compass (SEC) a point P sqrt(n) which will correspond to the number sqrt(n) on a Euclidean line.
2. Suppose we are given P0, P1, and P a where P a corresponds to the real number a>0. Give a construction with SEC of a point Psqrt(a) which will correspond to the number sqrt(a) on a Euclidean line.
3. Given points P0, P1, Px, and Py on a Euclidean line corresponding to the real numbers x>0 and y>0, give constructions with SEC for the following points.
| a) P x + y | b) P x - y | c) P x *y | d) P 1/x |
5. Suppose that d(A,B) = d(A',B') and that l is the perpendicular bisector of the line segment AA'. Let B'' be the reflection of B across l, i.e., B''= Tl(B). Prove that if B' is not equal to B'' then A' lies on the perpendicular bisector of the line segment B''B'.
1. Prove: Two of the medians of an isosceles triangle are congruent.
2. Prove: If two of the medians of a triangle are congruent then the triangle is isosceles.
3. Prove: The angle bisectors of congruent angles of an isosceles triangle are congruent.
4. Prove: If two of the angle bisectors of a triangle are congruent then the triangle is isosceles.
1. Use an affine line with P0 , P1 , and Pinf given. Show a construction for P1/2 and P2/3.
2. Use an affine line with P0 , P1 , and Pinf
given. Suppose x > 1.
Show a construction for Px2 and Px3 when
Px is known.
3. D is a circle with center N tangent to a line l at the point
O and C is a circle that passes through the N and is tangent to l at
O as well.
Suppose P is on l and PN intersect C = {Q}; Q' is on C so that
Q'Q is parallel to ON; and {P'} = NQ' intersect l.
Prove: a) P and Q are inverses with respect to the circle D.
b) P' and Q' are inverses with respect to the circle D.
c) P and P' are inverses with respect to the circle with center at
O and radius ON.
4. Suppose C is a circle with center O and D is a circle with O
an element of D.
Let I be the inversion transformation with respect to C.
Prove: There is a line l, where I(P) is an element of l for all P that are elements of D -{O}.