Suppose P is on l and PN intersect C = {Q}; Q' is on C so that Q'Q is parallel to ON; and {P'} = NQ' intersect l.
TEXTS: Fundamentals of Geometry by B. Meserve and J. Izzo,
A.W. (1969) -
ON LINE with HSU ONCORE
through Moodle.
The
Elements by Euclid, 3 volumes, edited by T.L. Heath, Dover
(1926)
Proof in Geometry by A.I Fetisov, Mir (1978)
Here's Looking at Euclid..., by J.Petit, Kaufmann (1985).
Flatland By E. Abbott, Dover.
| Week | Monday | Wednesday | Friday | Reading/Videos for the week. | Problems
Due on Wednesday of the next week | Math 480 Lab Assignments |
|---|---|---|---|---|---|---|
| 1 | 1/15 No Class |
1/17 1.1 Beginnings
|
1/19 |
M&I:1.1,
1.2
E:I Def'ns, etc. p153-5; Prop. 1-12,22,23,47 A:.Complete in three weeks |
Due:1/24 M&I p5:1-8,11 | |
| 2 | 1/22 The Pythagorean Theorem
Lab: Intro to Geometer's Sketchpad/ Wingeom |
1/24 Convexity defined. The Pythagorean Theorem 1.2 |
1/26 Guest Lecture on Euclid Here’s looking at Euclid |
M&I
1.2, 1.3
E: I Prop. 16, 27-32, 35-45. |
Due:
1/31 M&I: p10:1,2,5,10,11-13 Prove:The line segment connecting the midpoints of two sides of a triangle is parallel to the third side and is congruent to one half of the third side. [ HELP! Proof outline for the midpoint proposition.] |
Lab Exercises 1: Due: 1/29 Construct a sketch with technology of 1. Euclid's Proposition 1 in Book I. 2. Euclid's Proposition 2 in Book I. 3. One "proof" of the Pythagorean Theorem. |
| 3 | 1/29 Equidecomposable Polygons Constructions
Isometries 1.1 Def'ns- Objects 1.2 Constructions 1.3 Geometry: Constructions and numbers | 1/31 1.4 Continuity | 2/2 Breather: Start: Transformations - Isometries | M&I
1.3,1.4
E: III Prop. 1-3, 14-18, 20, 21, 10 F. Sect. 11, 25, 31 Watch Equidecomposable Polygons | Due: 2/7 [extended to2/14] M&I: p17:5, 8-11 p11: 16-19, 24, *27 Problem Set 1 | Lab Exercises 2: Due by : 2/5 Do Construction 3, 4, 6, 7, and 8 from Meserve and Izzo Section 1.2. BONUS:Show how to "add" two arbitrary triangles to create a single square. |
| 4 | 2/5 More on continuity and rational points. Similar triangles | 2/7 More on Cantor Start Inversion. |
2/9Orthogonal Circles Odds and ends. Transformations - Isometries. Coordinates. |
M&I:1.5,
1.6,
2.1
E: V def'ns 1-7;VI: prop 1&2 F. Sect. 32 |
Due 2/19 [Changed as of 2-9] M&I: p23: 9,10 (analytic proofs) M&I:1.6:1-12,17,18 Problem Set 2 |
Lab Exercises 3: Due 2/12 1. Construct a scalene triangle using Wingeometry. Illustrate how to do i) a translation by a given "vector", ii) a rotation by a given angle measure, and iii) reflections across a given line.. 2. Create a sketch that shows that the product of two reflections is either a translation or a rotation |
| 5 | 2/12 More Isometries: Coordinates and Transformations | 2/14 Isometries / |
2/16 coordinates/ |
M&I:
2.1, 2.2
E: V def'ns 1-7;VI: prop 1&2 E:IV Prop. 3-5 Isometries (Video # 2576 in Library) . |
Lab Exercises 4: Due 2/19 1. Draw a figure showing the product of three planar reflections as a glide reflection. 2. Draw a figure illustrating the effects of a central similarity on a triangle using magnification or dilation that is a) positive number >1, b) a positive number <1, and c) a negative number. |
|
| 6 | 2/19 classification | 2/21 More on Isometries |
2/23 .... Finish Classification of Planar Isometries. | M&I: 2.1,2.2 | Due 2/28 Extended to 3/7! Problem Set 3 (Isos Tri) [1 Point for every distinct correct proof of any of these problems.] |
Lab Exercises 5: Due 2/26.
1. Construct the inverse of a point with respect to a circle a) when the point is inside the circle; b) when the point is outside the circle. 2. Given a circle O and two interior points A and B, construct an orthogonal circle O' through A and B. 3. Draw two intersecting circles O and O' and measure the angle between them. |
| 7 Quiz #1 on Monday in class. |
2/26Isometries and symmetries Begin Affine Geometry Proportion and Similarity |
2/28 More on Similarity |
3/2 Inversion and Affine Geometry (planar coordinates) the Affine Line. | M&I: 2.2 again;3.1,3.2, 3.5 | Lab Exercise 6:
Due 3/5 1.Draw sketches for each of the following triangle coincidences: 1. Medians. 2. Angle Bisectors. 3. Altitudes. 4. Perpendicular Bisectors |
|
| 8 |
3/5 Visualizing the affine plane. Seeing the infinite. | 3/7 Affine geometry- Homogeneous coordinates and visualizing the affine plane. | 3/9 More on Homogeneous coordinates for the plane. | M&I:3.6,
3.4,3.7 View video (in Library #4376 ) on "Central similarities" from the Geometry Film Series. (10 minutes) View video (in Library #209 cass.2) on similarity (How big is too big? "scale and form") "On Size and Shape" from the For All Practical Purposes Series. (about 30 minutes) |
Lab Exercise 7: Due 3/19.
1. Inversion: Investigate and sketch the result of inversion on lines and circles in the plane with a given circle for inversion. When does a line invert to a line? When does a line invert to a circle? When does a circle invert to a line? when does a circle invert to a circle? Show sketches where each case occurs. [ Remember the inverse of the inverse is the original figure.] 2. Use inversion with respect to the circle OP to invert <BAC to <B'A'C'. Discuss briefly the effects of inversion on angles. 3. Draw a sketch of the affine plane showing the horizon line and label the lines X=1,2,-1, Y= 1,2,-1 and points (1,2) and (2,-1). |
|
| 9 Spring break | 3/12 No Class | 3/14 No Class | 3/16 No Class | |||
| 10 |
3/19 More on The affine Plane - A first look at a "Projective plane." Axioms, consistency, completeness and models. A non-euclidean universe. |
3/21 Begin Synthetic Geometry [Finite] Algebraic-projective geometry: Points and lines. Spatial and Planar |
3/23Axioms for 7 point geometry. Begin Synthetic Projective Geometry |
M&I :3.1, 3.2, 3.5, 3.6, 3.7; 4.1 |
Due : 3/28 M&I: 3.5: 1,3,4,5,10,11 3.6: 3,7-15 3.7: 1,4,7,10,13 Problem Set 4 |
Lab Exercise 8: Due 3/26 Draw a sketch for Desargues' theorem in the plane. Optional: Draw a spatial skectch for Desargues' Theorem |
| 11 |
3/26 Homogeneous Coordinates with Z2 and Z3 More on Finite Synthetic Geometry and models. Proof of Desargues' Theorem -Projective Geometry -Visual/algebraic and Synthetic..Axioms 1-6 Projective Planes. . |
3/28 More on the axioms of Projective Geometry.RP(2) as a model for synthetic geometry.
|
3/30 No Class.
CC Day. |
M&I:4.1, 4.2, 4.3, 2.4 | Due 4/11! - watch for additional problems. M&I:4.1:7,15,16; Prove P6 for RP(2); 4.2: 2,3, Supp:1 4.3: 1-6, Supp:1,5,6 |
Lab Exercise 9: Due 4/2 A.1. Construct a sketch showing ABC on a line perspectively related to A'B'C' on a second line with center O. 2. Construct a sketch of ABC on a line projectively (but not perspectively) related to A'B'C' on a second line. Show two centers and an intermediate line that gives the projectivity. B.1'. Draw a dual sketch for the figure in problem 1. 2'. Draw a dual sketch for the figure in problem 2. |
| 12 |
4/2Proofs of some basic projective geometric facts. Triangle Coincidences (Perpendicular Bisectors- the circumcenter) |
4/4 Applications of Projective Geometry Postulates.1-6 |
4/6 Desargue's Theorem and Duality | No Lab this week. | ||
| 13 |
4/9Conic Sections.
Pascal and More Duality |
4/11 Complete quadrangles Postulate 9.
Projective transformations. Perspectivities and Projectivities. |
4/13 Conics
Pascal's Theorem ? More on coordinates and transformations. |
M&I:
4.5,4.6(p94-97).4.7, p105-108 (Desargues' Thrm) |
Due : 4/18 M&I:4.5:2; 4.6:7,8,9; 4.7:4,7 4.10: 4,5,9,10 [Prove P9 for RP(2),optional] |
Lab Exercise 10: Due 4/16
Pascal's configuration: Hexagons inscribed in conics. Points of intersections of opposite sides lie on a single line. Construct a figure for Pascal's configuration with a) an ellipse , b)a parabola, and c) an hyperbola. |
| 14 |
4/16Projectivities. Perspective |
4/18 Transformations of lines with homogeneous coordinates. | 4/20 Projectivities in 3 space: More on Projective Line Transformations
with Coordinates. Begin Harmonic Sets and Construction of Coordinates. |
4.10, 5.4, 2.4
4.11 |
|
|
| 15 |
4/23Harmonic sets: uniqueness and construction of coordinates for a Projective
Line, Plane, Space. Projective generation of conics |
4/25 More on Transformations, Coordinates and Harmonic sets. . | 4/27Matrices for familiar Planar Projective Transformations. |
5.1,5.4;,5.2, 5.3,5.5, 5.7, 6.1, 6.2 | Due: 5/2 M&I:
4.10:1,3,6,7;
5.1:5; 5.4:1-8,10; 5.5: 2,3,7 |
Lab Exercise 11: Due 4/30 1.Draw a sketch showing H(AB,CD) and H(CD, AB). 2. Draw a sketch that shows that if H(AB,CD) and H(AB,CD*) then D= D*. |
| 16 |
4/30Conics revisited. Inversion and the final exam. Pascal's and Brianchon's Theorem. Quiz #3 |
5/2 5/5 Inversion angles, circles and lines. |
5/4The Big picture in Summary. . Student Presentations |
|
A Project Fair will be organized for displays and presentations during the last day of class. Details will be discussed later.
Guidelines for Preliminary Proposals:
| Tiling patterns - tesselation 3d tiling MC Escher perspective Curves: conics, etc. optical illusions knots fractals Origami Kaleidescope Symmetry The coloring problem Patterns in dance and other performance arts Flatland sequel (4d) | Maps Juggling structural Rigidity dimension Polyhedra bridgemaking (architecture) Models (3d puzzles) paper mache or clay mobiles sculpture A play - movie build three dimensional shapes power point performance website |
DEFINITIONS: A figure C is called convex if for any two
points in the figure, the line segment determined by those two points is
also contained in the figure.
That is, if A is a point of C and B is a point of C then the line segment
AB is a subset of C.
If F and G are figures then F int G is { X : X in F and
X in G }.
F int G is called the intersection of F and G.
If A is a family of figures (possibly infinite), then int
A
= { X : for every figure F in the family A, X is in F }.
int A is called the intersection of the family A.
-----------------------------------------------------------------
1. Prove: If F and G are convex figures , then F int G is a convex figure.
2. Give a counterexample for the converse of problem 1.
3. Prove: If A is a family of convex figures, then int A is a convex figure.
4. Prove: The line segment RS is convex. [ Refer to M & I pg.2.]
1. Suppose n is a natural number. Given P0 and P1 , prove by induction that you can construct with straight edge and compass (SEC) a point P sqrt(n) which will correspond to the number sqrt(n) on a Euclidean line.
2. Suppose we are given P0, P1, and P a where P a corresponds to the real number a>0. Give a construction with SEC of a point Psqrt(a) which will correspond to the number sqrt(a) on a Euclidean line.
3. Given points P0, P1, Px, and Py on a Euclidean line corresponding to the real numbers x>0 and y>0, give constructions with SEC for the following points.
| a) P x + y | b) P x - y | c) P x *y | d) P 1/x |
5. Suppose that d(A,B) = d(A',B') and that l is the perpendicular bisector of the line segment AA'. Let B'' be the reflection of B across l, i.e., B''= Tl(B). Prove that if B' is not equal to B'' then A' lies on the perpendicular bisector of the line segment.
1. Prove: Two of the medians of an isosceles triangle are congruent.
2. Prove: If two of the medians of a triangle are congruent then the triangle is isosceles.
3. Prove: The angle bisectors of congruent angles of an isosceles triangle are congruent.
4. Prove: If two of the angle bisectors of a triangle are congruent then the triangle is isosceles.
1. Use an affine line with P0 , P1 , and Pinf given. Show a construction for P1/2 and P2/3.
2. Use an affine line with P0 , P1 , and Pinf
given. Suppose x > 1.
Show a construction for Px2 and Px3 when
Px is known.
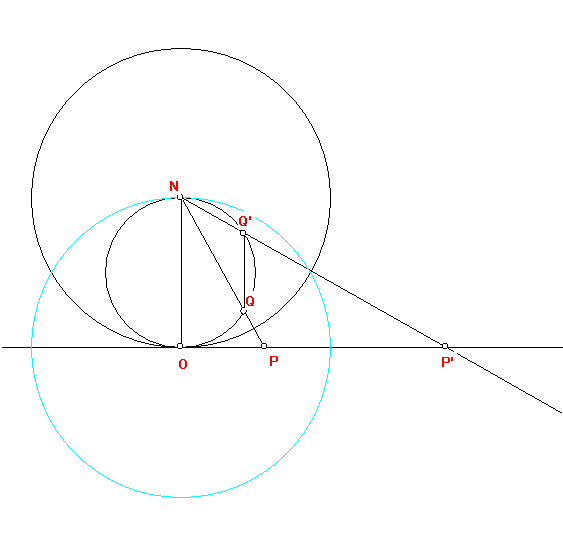
3. D is a circle with center N tangent to a line l at the point
O and C is a circle that passes through the N and is tangent to l at
O as well.
Suppose P is on l and PN intersect C = {Q}; Q' is on C so that
Q'Q is parallel to ON; and {P'} = NQ' intersect l.
Prove: a) P and Q are inverses with respect to the circle D.
b) P' and Q' are inverses with respect to the circle D.
c) P and P' are inverses with respect to the circle with center at
O and radius ON.
4. Suppose C is a circle with center O and D is a circle with O
an element of D.
Let I be the inversion transformation with respect to C.
Prove: There is a line l, where I(P) is an element of l for all P that are elements of D -{O}.