• Tuesday, Jan. 17. First class: Review of the structure of the course.
  
• Keys to success in this course:
• Active and regular participation.
• Open to new ways of organizing your thinking.
• Polya
• Solow
• Flashman :)
  
• Communicating often and regularly with others both in oral and written forms.
• Aim for EXCELLENCE!
  
• Keep a sense of humor .
  
• Activity Discussion (5-10 minutes):
• With a Partner discuss how Figure 1 can be used to "prove" : x + 1/x >= 2.
  One partner(A) should write the "proof" while the other partner(B) checks to see the writing fully reports their understanding.
  
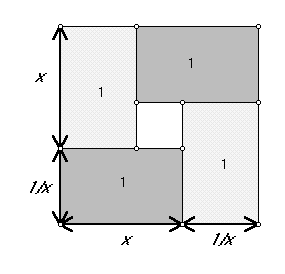  Figure 1

  ---

• With the same partner discuss how Figure 2 can be used to "prove" : x + 1/x >= 2.
  Now partner B should write the "proof" while the other partner (A) checks to see the writing fully reports their understanding.
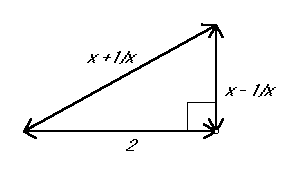  Figure 2

• [indicates material of interest not discussed in class.]
  
  
• Two concepts from Solow: Unification and Generalization.
  
• Examples of unification related solving equations such as 3x=15, 3x=24; then 3x=7 and 3x=N.
  
• Considered methods to solve these- especially 3x=15.
  
• guess and check.
•  "Guess": x=5.
  
• Check: 3*5 = 15 . Notice the check here resorts to common experience and background- as well as understanding of what constitutes a solution.
  
• list and search, 
  
• symbolic recognition of patterns, and
  
• algebraic solution using analysis. - "showing your work"
• consolidated version: x = 3x/3 = 15/3  = 5.
• "step by step"  version: 
  3x = 15
  1/3(3x) = 1/3 (15)
  x = 5
• "two column analysis"
  

  Statement	Reason
  3x = 15 1/3(3x) = 1/3 (15) x = 5	Given "Equals multiplied by equals give equals." 1/3(3x) = x; 1/3(15) = 5; "Transitivity of equality."

  
  This approach can be more thorough but can still leave out some details.
• Comparison with a calculus problem:  Find `int_0^1 x^3 dx`.
• An answer was proposed, 1/4, but there was no comparable way to "check this answer"
• Show the work: (1)`int_0^1 x^3 dx = 1/4x^4 |_0^1 = 1/4 - 0 = 1/4`
  Notice that some of this work is notational and the key step involves the "Fundamental Theorem of Calculus."
• Both problems are looking for a number as an answer that is described in a context, but the answer in the first one has a context that provides a way to "check", while the integration problem relies on a "theorem"  to justify its correctness.
• Comparison with (2) `int_{-1}^1 1/{ x^2}dx = -1/x |_{-1}^1 = -1 - (-1) = -2` [THIS IS AN ERROR!].
• Consideration of the area interpretation of the definite integral shows there must be something wrong with (2). The error lies in the application of the fundamental theorem - the hypothesis  that the function be continuous on a closed and bounded interval is not satisfied in (2) because  `1/{x^2}` is not continuous at `x=0`.
  
• Consider 3x=7.
  
• Both  a guess and check and analytic approach can work here. 
  
• It now becomes noteworthy that a solution for this problem may not exist if the only type of solution that makes sense is with natural numbers or integers. The solution here in the context of common arithmetic needs to have a number called "seven thirds."
• The context of a problem is important in understanding what an acceptable solution may be. This feature of the problem is sometimes left unstated or may be made explicit in the statement by words like "suppose x is a natural number.. " or " if x is any real number and... "
  
• Discuss the solution to the unification in Ax=B being solved by x= B/A.
  This follows the analytical process to arrive at a "closed form" solution.
• A generalization  of this problem in algebra :  Any (quadratic) polynomial  will have a root - possibly involving a complex number.
  

• another context to examine Unification and generalization.
• Show: if f(x) = x² then f '(3) = 6.
  
• use limits and the definition of the derivative.
• Move directly to a generalization that f '(a) = 2a.
• demonstrate directly again using the definition of the derivative and limits.
• Discuss: one could do similar work to show that if f(x)= x³ then f '(x) = 3x²
• one could arrive at a unification in the statement:
  If n is a natural number  and f(x) = xⁿ  then f '(x) = nx^n-1.
• If we think of n as a negative integer, say -4, then this is an example of generalization because the statement of the result extends to instances which are not covered by the common experience with 2 and 3.
• Likewise we can generalize the result to f(x) = x^r where r is any  fraction or more generally any real number, but a proof of that result might involve much more complicated arguments.
• Some fundamental discussion of sets....
  

  ---

• Briefly abstractions.

• Proofs:  Conditionals and "forward backward" 

  ---

• Some important sets that we will consider this term are as follows:

  the natural numbers	N	{1,2,3,...} or {0,1,2,3,...}
  the integers	Z	{0,1,-1,2,-2, ... }
  the rational numbers	Q	{ n/m where n and m are integers and m not 0}
  the real numbers	R	{ numbers that can be represented as decimals}

  The issue of being a member of  a set can be an issue of the nature of the set or the nature of the object. For example, we can consider sqrt(2) and ask, "is this a real number?" "Is this a rational number?" To determined if sqrt(2) is a member of R,we must have a way to determine this number as a decimal, that is to determine what digit would be in the kth decimal place for any k. Now this is possible through some estimaton procedures, though there is no closed form solution to determine the kth decimal place of the sqrt(2). On the other hand the sqrt(2) is not a member of the rational numbers. This is not because the rational numbers have a problem with the definition of that set, but is a question of mathematics to demonstrate that this number cannot be expressed as a ratio of integers as required by definition for membership in the set of rational numbers.

The nature of the subset relation. Focus on  the importance of recognizing the universal set involved in a discussion. Thus for example the set {x: 0 = 10 + 2x + x²} is an empty set if the universe is the real numbers, but contains two members if the universe is the set of complex numbers, C.

Some examples of sets of functions... C⁰ = { continuous real valued functions defined on all the real numbers} and C¹ = { differentiable real valued functions defined on all the real numbers}. The issue was whether these sets are equal.
 the subset relation : when set A is a subset of a set B. The definition of this term can be made in the form of an absolute statement: "every element of A is an element of B" or as a conditional statement: " if f is an element of  A then f is an element of B".
Observe that C¹  is a subset of C⁰. To prove this we suppose that f is a member of C¹and thus f is a differentiable function. It is a result of the calculus course that if a function is differentiable, then it is continuous. Thus f is a continuous function, which means it is a member of  C⁰ .

To consider the related issue, we ask "Is C⁰  a subset of C¹ ?"   Here the answer is : NO. To show that this is true we examined the function f (x)= |x|. This function is continuous for all real numbers, but is not differentiable at x = 0. This gives an instance where the conditional requirement for a subset fails, since the hypothesis is true for this function but the conclusion is false.  The example also shows why the absolute statement is false by giving a single member of C⁰ which is not a member of  C¹ . This lead to a discussion of the truth or falsity of conditional  and universal absolute statements in mathematics.

How to prove sets are equal using A={ 2, -2} and B = {x  : x²  = 2}.
(i) First, A is a subset of B. This is demonstrated by checking the equation of B for x = 2 and x = -2.
(ii) Then it is neceassary to show that B is a subset of A. For this we suppose x is an element of B, so that x²  = 2, and then x² - 2 = 0, so (x +2)(x-2) = 0. considering the last equation, together with the fact  that if the product of 2 real numbers is 0, then one of the factors is 0, we see that either x = -2 or x = 2. In either case, x  is a member of A.
 

• 
  
• The discussion focussed again on finding the truth values for complex statement using conjunction (and), disjunction (or), conditional (if..then), and negations (not).

We then discussed how simple statements appeared in compound statements using "and", "or", "if...then", and "not" and how to determine the truth of the compund sentence from knowing the truth of the simple statements. We examined wht there were 4 possible ways to have truth values for a pair of simple statements and how these would deteremine the truth value of a compund statement using a "truth table."

A	B	A and B	If A then B
T	T	T	T
T	F	F	F
F	T	F	T
F	F	F	T

This discussion will be continued next class.
 
• 2/3 The discussion focussed again on finding the truth values for complex statement using conjunction (and), disjunction (or), conditional (if..then), and negations (not).


A proposition is called a tautology if it is true without regard to the truth or falsity of any of its component statement.

A proposition A is said to be equivalent to another proposition B is the truth value of A is the same as the truth value of B for any choice of truth values for its primitive components.

We also considered the connective "if and only if", <->, called the biconditional. It has the following truth table:

A	B	A <->B
T	T	T
T	F	F
F	T	F
F	F	T

Proposition: The proposition  A is equivalent to the proposition B when and only when the proposition A<->B isa tautology.