| 8/29 | 8/31 | 9/1 | 10/2 | 10/3 | 10/5 | 10/6 | ||
| 9/5 | 9/7 | 9/8 | 10/9 | 10/10 | 10/12 | 10/13 | ||
| 9/11 | 9/12 | 9/14 | 9/15 | 10/16 | 10/17 | 10/19 | 10/20 | |
| 9/18 | 9/19 | 9/21 | 9/22 | 10/23 | 10/24 | 10/26 | 10/27 | |
| 9/25 | 9/26 | 9/28 | 9/29 | 10/30 | 10/31 | 11/1 | 11/2 |
- 8/29
- Class spent much time on problems from the review sheet related to functions.
- We examined f using a table of selected values:
- In summary, we examined f using a table of selected values:
- 8/31 ( and beyond!)
- Go over Background Analysis.
- Solutions:
- B: y=2x+5
- D: -9/10
- A: (x-1)/x^3
- D: x^2/(3y^9)
- D: 3x + 2 sqrt(15xy) + 5y
- C: $52
- D: 4
- SECTION 1.1
- Real numbers are decimals (possibly infinite and non-repeating)
- The number line. Points on the line correspond to real numbers.
- Absolute values.
- Example: |-2|=2; |sqrt(5)-5| = 5-sqrt(5).
- Example*: |2 + - 3| < |2| + |-3|
- Equality, inequality, and intervals.
- Solving a linear equation.
- Example. 3x+5=29:
- Solving a linear inequality.
- Example: 3x+5<29:
- Example: -2x < 10:
- Exponents and radicals:
- integer exponents:
- 2^3 = 2*2*2 = 8
- 2^0 = 1
- 2^-3 =1/ (2^3) = 1/8
- fraction exponents and roots
- 8^(1/3) = cube root of 8 = 2
- Properties:
- SAME BASE: Products, quotients, powers
- SAME POWER: Products. quotients.
- SECTION 1.2
- Multiplication and Factoring:
- a*(b+c)= a*b + a*c
- quadratic expressions (see text p 17)
- Roots and equations.
- Solving a quadratic equation.
- Example: x^2-5x + 6 = 0 :
- Example: x^2-5x + 6 = 0 :
- Fractions (Rational Expressions)
- Factor and "cancel"
- Common Denominators [Still to be reviewed.]
- Rationalizing expressions with roots. [Still to be reviewed.]
- SECTION 1.3
- Cartesian Coordiantes
Function notation was reviewed. Mapping(transformation) figures and graphs of functions were introduced .
2. For this problem let f be defined by f(x) = 5x2 + 3.
A. Find the following. Simplify you answer when possible.
i) f(1) = 5(1)2 + 3=8 iii) f(1+h)= 5(1+h)2 + 3= 8+10h+5h2
ii) f(h) = 5h2 + 3 iv) [f(1+h)-f(1)]/h = [10h +5h2 ]/h=h[10+5h]/h= 10 +5h
B. Find any number(s) z where f(z) = 23.
f(z)= 5z2 + 3= 23 ; 5z2 =20; ... z = 2 OR z = -2.
OR 5z2 - 20 = 0; 5(z+2)(z-2)=0; ... z = 2 OR z = -2.
C. For which values of x is f(x) < 23? Express your answer as an interval.
| x | f(x)= 5x2 +3 |
| 3 | 48 |
| 2 | 23 |
| 1 | 8 |
| 0 | 3 |
| -1 | 8 |
| -2 | 23 |
| -3 | 48 |
and a transformation (mapping) figure: 
Based on this we concluded that the solution was {x | -2<x<2}
= (-2,2).
After the analysis of the transformation figure we considered when x+2<0.... x< -2. We graphed this on a number line.
----------------0 +++++++++++++++ (x+2)
-2 0
Then we considered
f(x)=
5x2 + 3 < 23; so 5x2 - 20 < 0;
5(x+2)(x-2) < 0. We then scanned the line with information about the
factors (x+2) and (x-2) to investigate when the expression
5x2 - 20 would be positive, negative, or 0.
-------------------------0+++++++++ (x-2)
----------------0 +++++++++++++++ (x+2)
-2 0 2
+++++++++++0--------0+++++++++ 5(x+2)(x-2)
Thus -5x2 - 20 < 0 when 2<x<2... or x is in the interval (-2,2).
| x | f(x)= 5x2 +3 |
| 3 | 48 |
| 2 | 23 |
| 1 | 8 |
| 0 | 3 |
| -1 | 8 |
| -2 | 23 |
| -3 | 48 |
Numbers, Variables, Algebra Review 1.1&1.2
3x= 24; x =8.... check.
3x<24; x<8... x in the interval (-inf,8).
(No total check- but some confirming evidence!)
x > -5 .... x in the interval (-5, inf).
Factor (x-3)*(x-2)= 0
so either x-3=0 or x-2 = 0.
Thus x=3 or x=2 are solutions. CHECK!
x=[-(-5)+ or- sqrt( (-5)^2-4*1*6)]/2*1
=[ 5 + or - sqrt(25-24)]/2
= [5 + or - 1]/2
= 6/2 or 4/2
so x = 3 or 2.
- MATH 046 [CRN: 43406] is an algebra review Workshop for ELM & MPT Review. It is .5 units and meets
- Distance
- Example: eq'n of a circle with center at (1,2) and radius 3.
- SECTION 1.4 (some review here from last class)
- Slope
- m = (y2- y1)/ (x2-x1)
- Example: find slope of line through the points (4, 2) and (1,3):
- Interpret: m>0; m<0; m=0
- parallel non-vertical lines have the same slope.
- Equations for lines:
- Vertical:
- Example:X=3
- Non-vertical:
- Point- slope
- Example: m=5 through (2,3):
- slope- Y intercept
- Example: m=5 Y intercept is (0,7)
- General Equation:
- Example: find X and Y intercepts for 2X + 3Y - 6 = 0:
- 9/5 And 9/7 We did more on lines and ....
- SECTION 2.1 FUNCTIONS.
- What is a function?
- A function f is a correspondence (rule) which assigns to each member of the domain (source) set, x, a member of the co-domain (target) set, denoted f(x) .
- How are functions visualized?
- Mapping figures/transformation figures.
-
Graphs
- 9/8 starts here --
- How are functions defined?
- with a formula.
- with a table.
- with a graph.
- with a context.
- Suppose that C is the cost of producing X liters of OURBEST wine. C is a function of X
- Problem #8:
- We looked at the transformation figure from this data as well as the graph.
- We then examined this function's graph using WINPLOT.
-
- More examples of functions.
- Quadratic functions.
- Functions defined in cases.
- Polynomial functions.
- Rational functions.
- Power/root functions.
- A few details on functions- especially considering equilibrium for supply/demand.
- Demand p =f( xd) N.B. This reverses the more sensible relationship as xd being a function of p.
- Supply p =f( xs). N.B. This also reverses the more sensible relationship as xs being a function of p.
Friday Sept. 1 1900-2050 in SH 110 and
Saturday Sept. 2 0900-1550 SH 110.
This workshop should review much of what you will use in Math 106.
You will not need to take the test at the end of the workshop since you already have a code 40.
slope= m = (3-2)/(1-4) = 1/(-3) = - 1/3
Y-3=5(X-2) or Y=5(X-2)+3
Y=5X + 7
Set X= 0; 3Y=6; Y=2 so (0,2) is the Y intercept.
Set Y=0; 2X=6; X=3 so (3,0) is the X intercept.
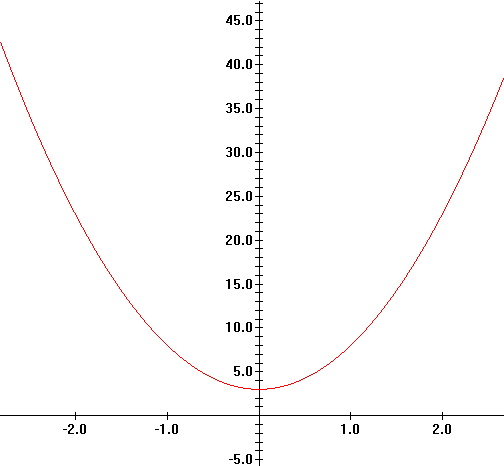
The function g is defined by assigning to the number x the value x2+5. This is expressed by the equation: g(x)=x2+5.
With this definition we have
g(0)=5, g(1)=6, g(-1)=6,g(2)=9, g(1/2)=21/4, g(t)=t2+5,
g(1+t)=(1+t)2+5, etc.
| x | f(x) |
| 2 | 5 |
| 1 | 3 |
| 0 | -2 |
| -1 | 4 |
| -2 | 0 |

The vertical line test: A graph measuring variables X and Y determines Y as a function of X if each vertical line meets the graph at at most one point.
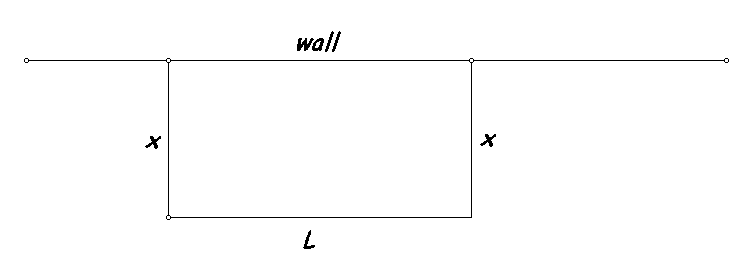
The wall is 200 meters long. We have 140 meters of fence. This is a constraint. In terms of the lengths measured x and L we have that 2x+L = 140. Thus L = 140 -2x.
The area, A, is found by multiplying x by L. Thus A = x (140-2x) = 2x(70-x). We made a table of some values of this function. We noted that 0<=x<=70.
| x | L | A |
| 10 | 120 | 1200 |
| 20 | 100 | 2000 |
| 70 | 0 | 0 |
| 60 | 20 | 1200 |
| 50 | 40 | 2000 |
This led to a conjecture from the symmetry that the largest value for the area, A, would occur when x = 35. in this case A=35*70=2450.
In fact, A = -2x2+140x but A also can be expressed
by A= -2(x-35)2 +2450. It should be clear from thinking about
this expression for A that A is at most 2450, since for any x other than
35, A will be the result of subtracting a positive number from 2450.
More on functions and Mathematical Modeling. (2.1 and 2.3)
- Use Winplot to graph examples of
these with parameters.
f(x)= Ax2 + Bx + C
i. s(x)= 2x+1 when x <3 ; -x+10 when x>=3
ii s(x)= 2x+1 when x <3 ; Ax+B when x>=3
cubic c(x)= Ax3 +Bx 2 + Cx + D
quartics q(x)= Ax4 + Bx3 + Cx 2 +Dx +E
R(x)=f(x)/g(x) where f and g are polynomials.
Examples: use polynomials above for f and g.
Example: Average cost= C(x)/x
examples: f(x)=sqrt(x); g(x)= x1/3