| 2/7 | 2/8 | 2/9 | 2/10 | 3/6 | 3/7 | 3/8 | 3/9 | 4/3 | 4/3 | 4/4 | 4/5 | 5/1 | 5/2 | 5/3 | 5/4 | ||||||||
| 1/19 | 1/20 | 2/14 | 2/15 | 2/16 | 2/17 | 3/13 | 3/14 | 3/15 | 3/16 | 4/10 | 4/11 | 4/12 | 4/13 | ||||||||||
| 1/24 | 1/25 | 1/26 | 1/27 | 2/21 | 2/22 | 2/23 | 2/24 | 3/20 | 3/21 | 3/22 | 3/23 | 4/17 | 4/18 | 4/19 | 4/20 | ||||||||
| 1/31 | 2/1 | 2/2 | 2/3 | 2/28 | 2/29 | 3/1 | 3/2 | 3/27 | 3/28 | 3/29 | 3/30 | 4/24 | 4/25 | 4/26 | 4/27 |
- 1/19 Numbers, Variables, Algebra Review 1.1&1.2
- Go over Background Analysis.
- Solutions:
- B: y=2x+5
- D: -9/10
- A: (x-1)/x^3
- D: x^2/(3y^9)
- D: 3x + 2 sqrt(15xy) + 5y
- C: $52
- D: 4
- SECTION 1.1
- Real numbers are decimals (possibly infinite and non-repeating)
- The number line. Points on the line correspond to real numbers.
- Absolute values.
- Example: |-2|=2; |sqrt(5)-5| = 5-sqrt(5).
- Example*: |2 + - 3| < |2| + |-3|
- Equality, inequality, and intervals.
- Solving a linear equation.
- Example. 3x+5=29:
- Solving a linear inequality.
- Example: 3x+5<29:
- Example: -2x < 10:
- Exponents and radicals:
- integer exponents:
- 2^3 = 2*2*2 = 8
- 2^0 = 1
- 2^-3 =1/ (2^3) = 1/8
- fraction exponents and roots
- 8^(1/3) = cube root of 8 = 2
- Properties:
- SAME BASE: Products, quotients, powers
- SAME POWER: Products. quotients.
- SECTION 1.2
- Multiplication and Factoring:
- a*(b+c)= a*b + a*c
- quadratic expressions (see text p 17)
- 1/20
- Class spent much time on problems from the review sheet related to functions.
- We also considered problem 115 on page 13.
- 1/24 start here:
- Summary of Chapter 1 in Calculus Applied to the Real World (on-line)
- We did several problems from 1.1 and 1.2... including problems about fractional and negative exponents, and factoring to solve a quadratic equation.
- [Also Reviewed interval notations]
- Roots and equations.
- Solving a quadratic equation.
- Example: x^2-5x + 6 = 0 :
- Example: x^2-5x + 6 = 0 :
- Fractions (Rational Expressions)
- Factor and "cancel"
- Common Denominators [Still to be reviewed.]
- Rationalizing expressions with roots. [Still to be reviewed.]
- SECTION 1.3
- Cartesian Coordiantes
- Distance
- Example: eq'n of a circle with center at (1,2) and radius 3.
- SECTION 1.4
- Slope
- m = (y2- y1)/ (x2-x1)
- Example: find slope of line through the points (4, 2) and (1,3):
- Interpret: m>0; m<0; m=0
- parallel non-vertical lines have the same slope.
- 1/25
- Start with a review of lines, then go on to functions (2.1)
- Equations for lines:
- Vertical:
- Example:X=3
- Non-vertical:
- Point- slope
- Example: m=5 through (2,3):
- slope- Y intercept
- Example: m=5 Y intercept is (0,7)
- General Equation:
- Example: find X and Y intercepts for 2X + 3Y - 6 = 0:
- SECTION 2.1 FUNCTIONS.
- What is a function?
- A function f is a correspondence (rule) which assigns to each member of the domain (source) set, x, a member of the co-domain (target) set, denoted f(x) .
- How are functions defined?
- with a formula.
- with a table.
- with a graph.
- with a context.
- How are functions visualized?
- Mapping figures/transformation figures.
- Graphs.
- 1/26
- Problem #8 was done !
- We looked at the transformation figure from this data as well as the graph.
- We then examined this function's graph using WINPLOT.
- At the end of class we looked briefly at two problems on functions and transformation figures.
- 1/27
- We looked at problems from today's and the previous day's assignment.
- More on functions and Mathematical Modeling. (2.1 and 2.3)
- More examples of functions.
- Quadratic functions.
- && Functions defined in cases.
- Polynomial functions.
- && Rational functions.
- && Power/root functions.
- 1/31
- Finish a few details on functions- especially considering equilibrium for supply/demand.
- Demand p =f( xd) N.B. This reverses the more sensible relationship as xd being a function of p.
- Supply p =f( xs). N.B. This also reverses the more sensible relationship as xs being a function of p.
- Begin Rates and slopes and margins.
- average velocity (rate), slope of a secant line, marginal cost/unit for an indivisible commodity.
- 2/1
- Instantaneous velocity, slope of a tangent line; marginal cost/unit for a divisible commodity .
- Average velocity-Instantaneous velocity
- Average rate of price change wrt time- instantaneous rate of price change wrt time
- average marginal cost per unit- marginal cost per unit
- slope of secant line to curve- slope of tangent line to a curve.
- Slopes of tangents and secants, instantaneous rates and average rates. Estimation and limits.
- Suppose Y= f(X). Consider X=a and X=a+h. These correspond to 2 points on the the graph of f,
- When h is very close to 0, h -> 0,
- Example: f(x)= 100-16x2. Find the slope of the tangent to the graph at when x=2.
- Example: Suppose S =f(t) feet where t is measured in seconds with f from the previous example. Then the instantaneous velocity of the object at time 2 seconds is -64 feet per second.
- 2/2
- Continued discussion of the tangent line/instantaneous velocity/rate problem.
- The equation of the tangent line when x=2 is given by
- To find the slope of the tangent at a more general contect when x=a:
- This is consistent with the result when x=2.
- Limit notation for expressing this work:....
- Do this for x...
- 2/3 See the text chapter 2 summary and Section 3.1 for examples of what we did today.
- We talked more about the definition of the derivative and finding the derivative using algebra and thinking.
- We started an examination of the calculus of derivatives using constants. powers, constant multiples, and sums.
- We started to use Leibniz notation for the derivative.
- 2/7 More on the rules of the calculus for derivatives.
- Justifications for some rules: constants, powers (integers, square roots), constant multiples, sums.
- Start product and quotient rules.
- 2/8 More on the rules of the calculus for derivatives.
- Justifications and interpetations of the derivatives of powers, constant multiples and sums.
- Introduced Product Rule.
- 2/9 More on the rules of the calculus for derivatives.
- Demonstration of the product rule's proof.
- Quotient rule introduced and justified based on the product rule.
- 2/10 More on the rules of the calculus for derivatives.
- More work with the quotient rule.
- If Q(x) = 1/ P(x) then by applying the quotient rule we have
- If f(x) = 1/ x n = x -n then f '(x) = -nx n-1 / x 2n = -n x -n-1.
- If C(x) = the total cost for producing x units, C'(x) is the marginal cost for producing one more unit.
- Using time, t , position of a car, s , and the consumption of gas, g, during a trip we started a consideration of the chain rule: dg/dt = dg/ds * ds/dt.
- 2/14 Class cancelled (power failure)
- 2/15 More on the chain rule. Marginal cost, reveues, and profit.
- 2/16
- Higher order derivatives.
- Implicit differention.
- 2/17
- Related Rates
- The differential
- Elasticity of demand.
- Suppose x= f(p). We wish to consider how a small change in price, h, effects the change in quantity demanded on a percentage basis... i.e.
- The elasticity of demand is defined to be E(p) = -p*f '(p) / f(p) = - p / x * dx/dp.
3x= 24; x =8.... check.
3x<24; x<8... x in the interval (-inf,8).
(No total check- but some confirming evidence!)
x > -5 .... x in the interval (-5, inf).
Function notation was reviewed. Mapping(transformation) figures and graphs of functions were introduced .
2. For this problem let f be defined by f(x) = 5x2 + 3.
A. Find the following. Simplify you answer when possible.
i) f(1) = 5(1)2 + 3=8 iii) f(1+h)= 5(1+h)2 + 3= 8+10h+5h2
ii) f(h) = 5h2 + 3 iv) [f(1+h)-f(1)]/h = [10h +5h2 ]/h=h[10+5h]/h= 10 +5h
B. Find any number(s) z where f(z) = 23.
f(z)= 5z2 + 3= 23 ; 5z2 =20; ... z = 2 OR z = -2.
C. For which values of x is f(x) < 23? Express your answer as an interval.
f(x)= 5x2 + 3 < 23; so 5x2 < 20; x2 < 4; so -2<x<2... or x is in the interval (-2,2).
5. Boyle's law states that , for a certain gas P*V = 320, where P is
pressure and V is volume.
A. Draw a complete graph representing this situation.
Label your axes and write an equation for each asymptote.
Make a table of values for P and V using P=320/V and P>0, V>0.
| V | P |
| 80 | 4 |
| 160 | 2 |
| 320 | 1 |
| 640 | .5 |
Now use these data points to sketch the graph.
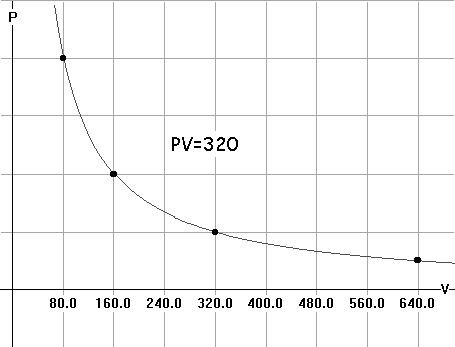
B. If 8 < V < 40, what are the corresponding values of
P?
Notice that when V=8, P = 40 and when V=40, P= 8. So as V varies from
8 to 40, P varies from 40 to 8.
C: the monthly commission. X: the total sales .
C= .15 (X-12000) >= 1000; so X-12000>=1000/.15 and thus X >= 12000 + 1000/.15 = 12000 +20000/3= $18667
Factor (x-3)*(x-2)= 0
so either x-3=0 or x-2 = 0.
Thus x=3 or x=2 are solutions. CHECK!
x=[-(-5)+ or- sqrt( (-5)^2-4*1*6)]/2*1
=[ 5 + or - sqrt(25-24)]/2
= [5 + or - 1]/2
= 6/2 or 4/2
so x = 3 or 2.
slope= m = (3-2)/(1-4) = 1/(-3) = - 1/3
Y-3=5(X-2) or Y=5(X-2)+3
Y=5X + 7
Set X= 0; 3Y=6; Y=2 so (0,2) is the Y intercept.
Set Y=0; 2X=6; X=3 so (3,0) is the X intercept.
The function g is defined by assigning to the number x the value x2+5. This is expressed by the equation: g(x)=x2+5.
With this definition we have
g(0)=5, g(1)=6, g(-1)=6,g(2)=9, g(1/2)=21/4, g(t)=t2+5,
g(1+t)=(1+t)2+5, etc.
| x | f(x) |
| 2 | 5 |
| 1 | 3 |
| 0 | -2 |
| -1 | 4 |
| -2 | 0 |

The vertical line test: A graph measuring variables X and Y determines Y as a function of X if each vertical line meets the graph at at most one point.
Suppose that C is the cost of producing X liters of OURBEST wine. C is a function of X
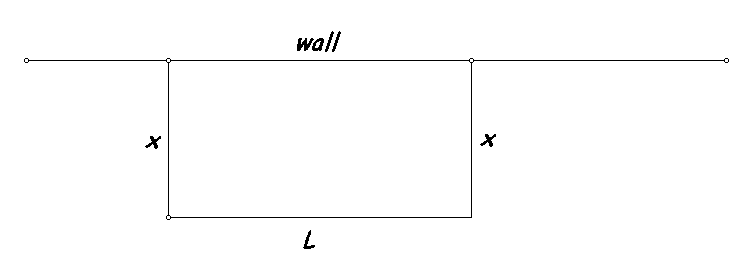
The wall is 200 meters long. We have 140 meters of fence. This is a constraint. In terms of the lengths measured x and L we have that 2x+L = 140. Thus L = 140 -2x.
The area, A, is found by multiplying x by L. Thus A = x (140-2x) = 2x(70-x). We made a table of some values of this function. We noted that 0<=x<=70.
| x | L | A |
| 10 | 120 | 1200 |
| 20 | 100 | 2000 |
| 70 | 0 | 0 |
| 60 | 20 | 1200 |
| 50 | 40 | 2000 |
This led to a conjecture from the symmetry that the largest value for the area, A, would occur when x = 35. in this case A=35*70=2450.
In fact, A = -2x2+140x but A also can be expressed
by A= -2(x-35)2 +2450. It should be clear from thinking about
this expression for A that A is at most 2450, since for any x other than
35, A will be the result of subtracting a positive number from 2450.
Using these problems we reviewed several aspects of functions as indicated below by &&.
Use Winplot to graph examples of these with parameters.
f(x)= Ax2 + Bx + C
i. s(x)= 2x+1 when x <3 ; -x+10 when x>=3
ii s(x)= 2x+1 when x <3 ; Ax+B when x>=3
cubic c(x)= Ax3 +Bx 2 + Cx + D
quartics q(x)= Ax4 + Bx3 + Cx 2 +Dx +E
R(x)=f(x)/g(x) where f and g are polynomials.
Examples: use polynomials above for f and g.
Example: Average cost= C(x)/x
examples: f(x)=sqrt(x); g(x)= x1/3
Average Velocity Example: Suppose
position of an anvil falling from a 100 foot cliff is a function of time,
S = -16t2 +100 feet
at time t seconds.
The position at times t=1 and t=2.
Find the average velocity during
the time interval [1,2].
Solution: S(1) = -16+100 = 84;
S(2) = -16*4 + 100 = 36.
Average velocity = change in position/
change in time = [S(2)-S(1)]/[2-1] = (36-84)/(2-1) = -48 ft/sec.
Note: The negative velocity indicates
the anvil is falling down. The average speed of the anvil is 48 ft/sec.
- Use Winplot to graph examples.
(a, f(a)) and (a+h, f(a+h)). The line connecting these two points ids called the secant line.
The slope of the secant line is [f(a+h)-f(a)]/h.
This is also the average velocity of an object moving on a straight line with its position S = f(t) at time t for the time interval between time time t= a and time t=a+h.
the value of [f(a+h)-f(a)]/h will approximate the slope of the line tangent to the graph of f at the point (a,f(a). It will also approximate the instantaneous velocity of the object moving on the straight line at time t=a.
Solution: . First find the slope of the secant line determined by X=2 and X= 2+h.
f(a)=100-16a2 ; a =2 so f(2) = 100 - 16*4= 36.
f(a+h)= f(2+h) = 100 -16(2+h) 2 = 100 - 64 - 64h -16h2 = 36 -64h -16 h2 ;
Thus f(a+h) - f(a) = -64h -16h2 = h(-64-16h) and [f(a+h)-f(a)]/h = -64 -16h.
Now: THINK! When h ->0, this slope = -64-16h -> -64. Thus the slope is -64.
y=-64(x-2) + 36.

Consider the quotient [f(a+h)-f(a)]/h using the general choice of a in place of the specific value x=2:
f(a+h) =100 - 16(a+h)2 = 100 -16a2 -32ah-16h2
f(a) =100 - 16 a2
so
f(a+h)-f(a)= -32ah - 16h2 = (-32a-16h)h
and thus [f(a+h)-f(a)]/h= -32a -16h.
Now considering what happens when h is close to 0, we have the slopes of the secants =-32a-16h -> -32a.
Q'(x)= -P'(x)/[P(x)]2.
If we denote by C (x) = C(x)/x = the average cost for producing x units, then by the quotient rule C '(x) = [x C'(x) -C(x)]/x 2 is the marginal average cost for producing one more unit.
[Percent change in quantity demand] / [ Percent change in unit price]
or [ {f(p+h) - f(p) }/f(p) *100] / [ h/p *100] .
When h is small this is approximately f '(p) /(f(p)/p) = p*f '(p) / f(p).