• Dissections (Junkyard)
• Dissection Animations
• The Puzzling World of Polyhedral Dissections by Stewart T. Coffin.

 
• Equidecomposable polygons (translation from Portugese)

 

 
 
 

Recall:
   * Scissors congruence: A sc= B means figure A can be cut into pieces that can be reassembled to form figure B.
      This is also described using the word "equidecomposable".  "A and B are equdecomposable to B."

•  SC =  is a reflexive, symmetric, and transitive relation. [like congruence and similarity in geometry and equality in arithmetic]
• Theorem I : A sc= B implies Area(A) = Area(B)
• Theorem II [The converse of Theoerm I!]: Area(A) = Area(B)  implies A sc= B !!
• Simple cases as evidence and a foundation for building toward the proof of Theorem II.:
• A triangle is SC to a rectangle. Activity from last class.

 
• Problem[ "lemma"] - To find a square with the same area as a given rectangle. Activity from last class.
• A rectangle is SC to a square.  Activity from last class.

 
• Two squares are SC to a single square. The Pythagorean Puzzle

 
• Triangulation .: Any polygon can be decomposed into triangles!
• A polygon is SC to a square.

 
• If two polygons have equal area, then they are SC to the same square!

Hence, any two polycons of equal area are Scissors congruent.

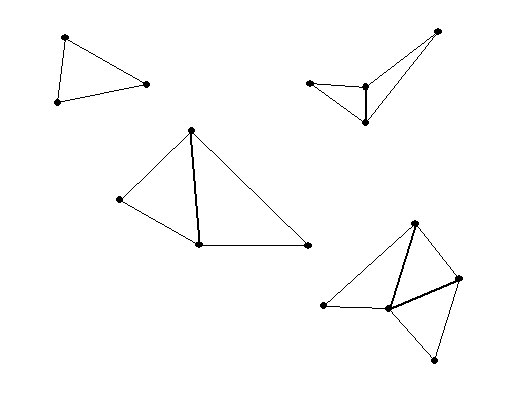
Consider a polygon with n sides.

When n = 3 this is a triangle, n=4, a quadrilateral, or when n= 5, a pentagon.

The sum of the measures of the interior angles of a triangle is 180 degrees.
Question:What about a quadrilateral? and a pentagon?  or an n sided polygon  ( an "n -gon")?

 

From the figure we can see that for a quadrilateral (n =4), which can be dissected into two triangles,
the sum is 2*180= 360 degrees.
And for a pentagon (n=5) which can be dissected into 3 triangles, the sum is 3*180=540 degrees.

A regular  polygon is a polygon where the sides are all of equal length and the angles are all congruent (or of equal measure).

For a triangle, the individual angle is 180/ 3 = 60 degrees.
For a square, the individual angle is 360 / 4 = 90 degrees.
For a regular pentagon.... 540/5=108  degrees.

Now for a HEXAGON (6 sides) the sum of the angles is (6-2)* 180= 4*180 = 720 degrees.
So ... for a REGULAR HEXAGON,  the individual angle is  720/6= 120 degrees.

1. Dissection of the plane--- Tilings of the plane.
2. Activity: Tile plane with playing cards.