Tuesday, May 3
Projective geometry: The study of properties of figures that are related by projections... perspectivities and projectivities.
Examples: The projection of a line is a line. The point of intersection
of two lines will project to the point of intersection of the projected
lines.
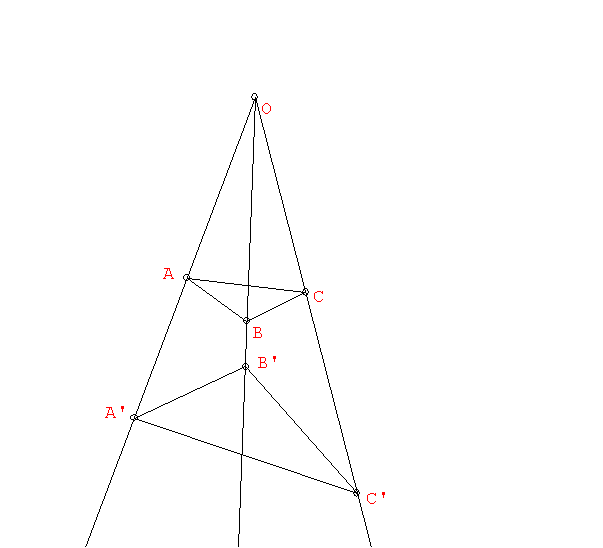
Desargues' Theorem in Space:
We define a perspective relation:
Two points P and P' are perspectively
related by the center O if O is on the line PP" . Two triangles ABC and
A'B'C' are perspectively related by the center O if O is on the lines AA',
BB', and CC'.
Maps of the earth that use Projection:
Perpective between planes in Space!
How to see the Infinite using Projective geometry.
Seeing the horizon on a plane.... a line of ideal/infinite points.
How parallel lines "meet" on the horizon.
Not done:Use Rope and lines on floor with an image plane to see parallels meet --- where is the horizon?
Using coordinates to draw in perspective.
Activity (not done): Creating coordinates in the projective plane and using them
to transfer a circle to the projective plane as an ellipse.
What do the conics look like in a perspective drawing or in the projective plane?
What is projection for Flatland?
Center of projection/ perspective.
[ compare with similarity].
Correspondences: Activity:
Circle to line and line to Circle!
How to see the Infinite using Projective geometry.
Conics in Cartesian coordinate geometry trasnfered to the projective plane.
Equations for conics in coordinate geometry.
Using coordinates to draw in perspective.
What do the conic look like in a perspective drawing or in the projective plane?
What is projection for Flatland?
Center of projection/ perspective.
How to see the Infinite using Projective geometry.
Activity on Perspective and Projective relations between points on lines.
Perpective between planes in Space!
Seeing the horizon on a plane.... a line of ideal/infinite points.
How parallel lines "meet" on the horizon.
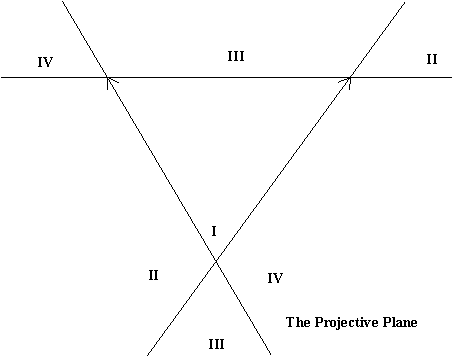
What is the Projective Plane?
How do we see curves in perspective, drawn in the Projective Plane?
Desargues' Theorem revisited.