Wednesday April 30
Discuss the last week's assignment on surfaces and review.
Last Class: Classification of surfaces almost done!
Euler's Formula for the plane
or the sphere:
Theorem: For any connected network in the plane,
The number 2 is called the "Euler characteristic
for the plane." ( and the sphere).

A sphere
A torus
[Activity:Graphs on the torus]
Games and puzzles on the torus and the klein bottle.
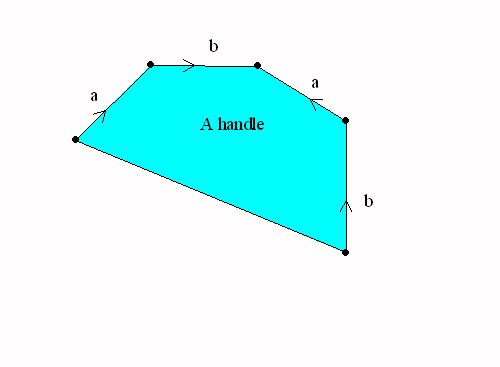
Spheres with handles:
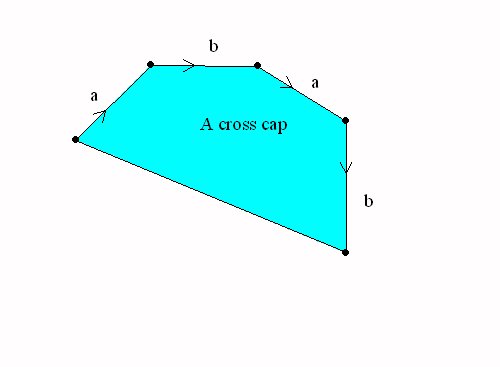
Spheres with cross caps
Visualizations of surfaces by
flattened maps - cut apart models.
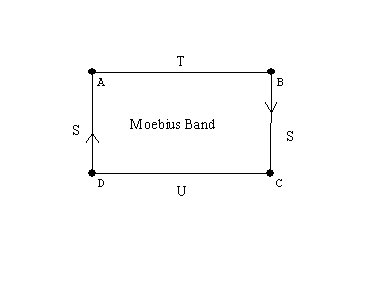
A cylinder, a mobius band, the torus, the Klein bottle, the projective
plane.
Handles and cross-caps
attached to the sphere.
|
|
| A sphere with a handle = a torus |
A Sphere with a cross cap = the projective plane |
The Topological Classification of "closed surfaces."
Every connected closed and bounded surface is topologically equivalent to a sphere with handles and crosscaps attached.