Wednesday April 30

    Discuss the last week's assignment on surfaces and review.

    Last Class: Classification of surfaces almost done!

Review examples: A closed disc, an open disc, a plane, an annulus- cylinder, a mobius band;

     


    A sphere

    A torus


  Torus

    [Activity:Graphs on the torus]

Games and puzzles on the torus and the klein bottle.



 

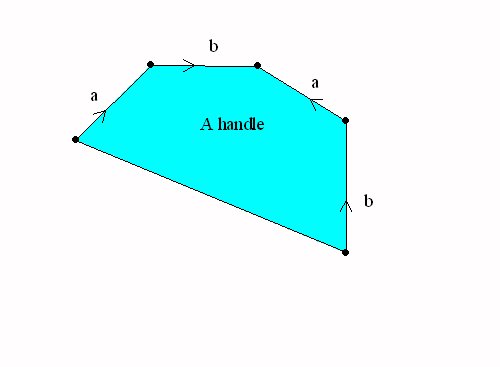
    Spheres with handles:

Boy's Surface

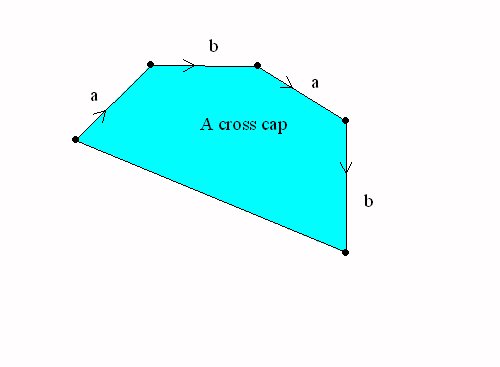
    Spheres with cross caps

Crosscap .

    Visualizations of surfaces by flattened maps - cut apart models.
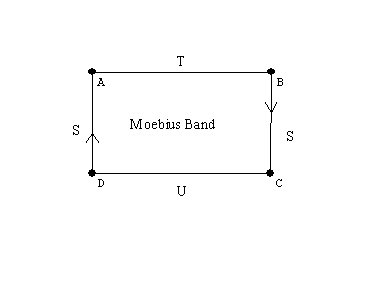
    A cylinder, a mobius band, the torus, the Klein bottle, the projective plane.

    Handles and cross-caps  attached to the sphere.

Closed Surfaces: Handles and cross-caps  attached to the sphere.
A sphere with a handle = a torus
  A Sphere with a cross cap = the projective plane


    The Topological Classification of "closed surfaces."

    Every connected closed and bounded surface is topologically equivalent to a sphere with handles and crosscaps attached.

    Proof (Last class!)....



The Euler Characteristic of A Surface.

The classification of surfaces determines the euler characteristic of each surface.

If the surface is orientable, it is a sphere with n handles, so V-E+R = 1 - 2n +1 = 2-2n.  For example the torus has euler characteristic 2-2*1=0.
If the surface is orientable - it's Euler characteristic is enough to identify the surface.
 
If the surface is non-orientable, then is it a sphere with k crosscaps and n handles, so the euler characteristic is V-E+R = 1 - (k+2n) +1 =2 -2n -k.
Notice that a sphere with two cross caps has euler characteristic 0, the same as the torus. But this was the euler characteristic of the Klein Bottle. So we should be able to recognize the Klein bottle as a sphere with two cross caps.
This can be done by a single normalization of one pair of edges with the same  orientation.


More topics for today: Continuum Hypothesis?
Smullyan puzzles  activities.