Thursday, March 25
More on the fourth dimension:
A progression: Point and segment on a line, line segment and square in
a plane (2-dim), square and a cube in space (3-dim), cube and a
"hypercube" in hyperspace (4-dim)
The Hypercube
and coordinates:
What do we measure? How does this determine "dimension?"
For a Line segment we can use one number to indicate distance and direction
from a single point: 0 .... 1
For a Square we use two "coordinates" and we can identify the vertices of
the square: (0,0), (1,0), (0,1),(1,1)
For a Cube we
use three "coordinates" and we can identify the vertices of the cube with
qualities such as "left..right", "up... down", and "front ... back":
(0,0,0) ,
(1,0,0), (0,1,0),(1,1,0)
(0,0,1),
(1,0,1), (0,1,1),
(1,1,1)
For a Hypercube....we
use four "coordinates" and we can identify the vertices of the hypercube
with qualities such
as "left..right", "up... down", and "front ... back" and "inside... outside":
(0,0,0,0)
, (1,0,0,0), (0,1,0,0),(1,1,0,0)
(0,0,1,0),
(1,0,1,0), (0,1,1,0),
(1,1,1,0)
(0,0,0,1) ,
(1,0,0,1), (0,1,0,1),(1,1,0,1)
(0,0,1,1),
(1,0,1,1), (0,1,1,1),
(1,1,1,1)
Another four dimensional object:
The hyper simplex!
point
line segment
triangle
tetrahedron ("simplex")
Cards and the fourth dimension.
(clubs,diamonds,hearts,spades)
(1,1,1,1) (0,0,0,0)
(1,1,0,1) (0,0,1,0)
(0,1,0,1)
(1,0,1,0)
(0,0,0,1)
(1,1,1,0)
(0,0,0,0)
(1,1,1,1)
Hamiltonian Tour: move through each vertex once and only once.
13 cards "bridge hand" : (5,3,0,5) (4,2,6,1)
Other ways to think about the hypercube:
video
Other ways to use coordinates:
Maps
Coordinates for "earth" - the sphere
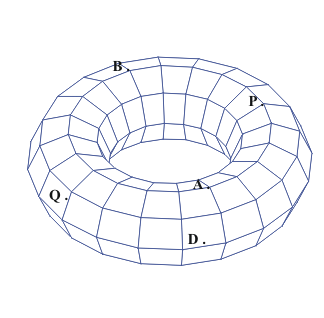
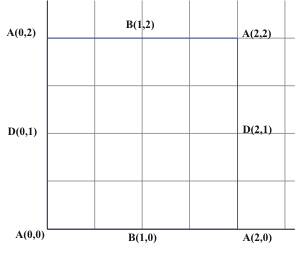
Coordinates for the torus!
The Tower of Hanoi
(clubs,diamonds,hearts,spades)
(1,1,1,1) (0,0,0,0)
(1,1,0,1) (0,0,1,0)
(0,1,0,1)
(1,0,1,0)
(0,0,0,1)
(1,1,1,0)
(0,0,0,0)
(1,1,1,1)
Hamiltonian Tour: move through each vertex once and only once.
13 cards : (5,3,0,5) (4,2,6,1)
Other ways to think about the hypercube:
video
Other ways to use coordinates:
The Tower of Hanoi
The general problem: (illustrated with three objects)
Move objects that have an order (size) from one place to another using only
a third place for "storage". No larger object can be placed on top of a smaller
object during the move. Move only one object at a time!
Solution of the 3 Tower of Hanoi Puzzle.
(Using playing cards 1,2,3)
Card- Post Changes to cards 0-1 Changes to
cards
(0, 0, 0)
(0, 0, 0)
1. 1 → B (1, 0, 0)
(1, 0, 0)
2. 2 → C (1, 1, 0)
(1, 1, 0)
3. 1 → C (2, 1, 0)
(0, 1, 0)
4. 3 → B (2, 1, 1)
(0, 1, 1)
5. 1 → A (3, 1, 1)
(1, 1, 1)
6. 2 → B (3, 2, 1)
(1, 0, 1)
7. 1 → B (4, 2, 1)
(0, 0, 1)
Record your moves. Assume that 1 represents the ace and the posts are labelled
A, B and C.
[Use the seven moves below from the 3 tower puzzle as a start.] Record also
the coordinates in 4 dimensional space for the number of changes made to
the 4 cards and the 0-1 switches.
Solution of the 4 Tower of Hanoi Puzzle.
Card→Post Changes to cards
0-1 Switches to cards
(0, 0, 0, 0) (0,
0, 0, 0)
1. 1 → B (1, 0, 0, 0)
(1, 0, 0, 0)
2. 2 → C (1, 1, 0, 0)
(1, 1, 0, 0)
3. 1 → C (2, 1, 0, 0)
(0, 1, 0, 0)
4. 3 → B (2, 1, 1, 0)
(0, 1, 1, 0)
5. 1 → A (3, 1, 1, 0)
(1, 1, 1, 0)
6. 2 → B (3, 2, 1, 0)
(1, 0, 1, 0)
7. 1 → B (4, 2, 1, 0)
(0, 0, 1, 0)
8.
9.
10
11.
12.
13.
14.
15.
This finds a Hamiltonian tour on the hypercube!
Four puzzle Competition: elimination tournament? Prize?
2. Discuss how you would solve the 5-tower puzzle.
Move 4, then 1, then 4... so
How many moves would it take to solve the 5-tower puzzle?
15 + 1 + 15 =31 moves.
A 5 dimensional hypercube would use coordinates
( a,b,c,d,e) with a,b,c,d, or e either 0 or 1.... giving 2*2*2*2*2 = 32 vertices.
How many moves would it take to solve the 6-tower puzzle?
31 + 31 +1= 63
Based on the actual time it takes you now to do the 4-tower, how long do
you think it would take you to do the 8-tower puzzle? Discuss the reasoning
for your estimate briefly.
we used 10 seconds for 15 moves ( our fastest player's time!)
2 *2 *2* 2* 2* 2* 2* 2 -1=255 moves
255 *10/ 15 = about 170 second = about 3minute
More on the
Hypercube
and higher dimensions:
For a Hypercube....we
use four "coordinates" and we can identify the vertices of the hypercube with
qualities such as "left..right", "up... down", and "front ... back" and "inside...
outside": (0,0,0,0) ,
(1,0,0,0), (0,1,0,0),(1,1,0,0)
(0,0,1,0),
(1,0,1,0), (0,1,1,0),
(1,1,1,0)
(0,0,0,1) ,
(1,0,0,1), (0,1,0,1),(1,1,0,1)
(0,0,1,1),
(1,0,1,1), (0,1,1,1),
(1,1,1,1)
Note: Dali use of the hypercube unfolded.
[connection w/ Banchoff}
What about a 5 dimensional cube?
Another five dimensional object:
The 5 dimensional hyper simplex!
point
line segment
triangle
tetrahedron ("simplex")
4 dimensional hypersimplex
Maps
Coordinates for "earth" - the sphere
Coordinates for the torus!
Activity for maps on Torus.
Locate P and Q on the map! give their coordinates.