An isometry is a transformation that preserves the distance between
points.
reflections, rotations, translations, and glide reflections.
The Product of isometries:
The product of two reflections is either a rotation (if the axes of the reflection intersect) or a translation (if the axes of the reflection are parallel).
We have discussed four isometries:
reflections, rotations, translations, and glide reflections.
The Product of isometries:
The product of two reflections is either a rotation (if the axes of the reflection intersect) or a translation (if the axes of the reflection are parallel).
Wingeometry demonstration for reflection- one and two reflections
Any plane isometry is
either a reflection
or the product of two or three reflections.
What about 3 reflections?
Three reflections = reflection or glide reflection
Key idea- The product of two reflections is "flexible."
discuss
basic idea:
Reflection is related to "perpendicular bisector" of PP'
With a triangle the 3 vertices ABC -> A'B'C' may be related to at
most
3 lines of reflection.
Proof: Click here!
What about 3 reflections?
Three reflections = reflection or glide reflection
Key idea- The product of two reflections is "flexible."
Space:
How do we understand objects in space?
How can the Flatlander experience the sphere and space?
The simplest three dimensional figure has 4 points not all in the same plane: three point determine a plane- so a fourth point not in that plane will need "space" to make sense. These four points determine a tetrahedron.
The simplest three dimensional figure has 4 points not all in the same plane: three point determine a plane- so a fourth point not in that plane will need "space" to make sense. These four points determine a tetrahedron.
Fold downs- flattened figures:
Consider how the tetrahedron can be assembled from folded down triangles.
Consider how the cube can be assembled from folded down squares in two different configurations: a cross or a "zig-zag."
Consider how the tetrahedron can be assembled from folded down triangles.
Consider how the cube can be assembled from folded down squares in two different configurations: a cross or a "zig-zag."
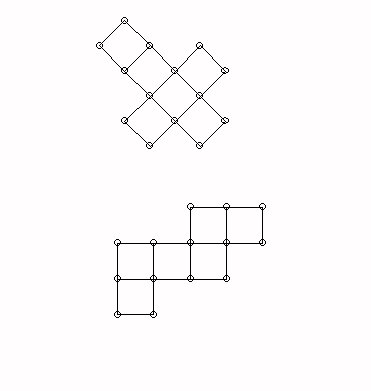
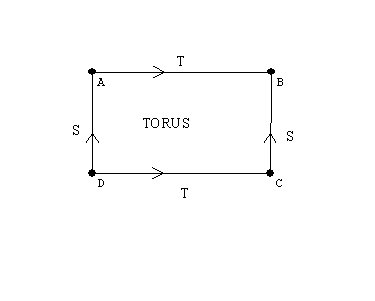
What does a folded down flattened torus look like?
A rectangle with opposite sides resulting from cutting the torus open making a cylinder and then cutting the cylinder along its length.
A torus
How to know the mathematics is "right'?
Proof starting with Euclid.
Proposition 1 Book 1
Euclid's tools. Proposition 1 and Proposition 2
Models for possibilities and impossibilities.
A model for the plane geometry of Euclid:
The basis for this model is understanding numbers!
Points: (a,b) where a and b are rational numbers.
Lines: Sets of points (x,y) that satisfy an equation Ax + By = C where A,B, and C are rational numbers and not all are 0.
Circles: Sets of points (x,y) that satisfy an equation of the form (x-A)2 + (y-B)2 = C where A,B, and C are rational numbers and C > 0.
Basic Facts: If I can build a model for the properties - the properties are consistent ( no contradictions or absurdities)
If I assume that something is possible (or exists) and arrive at a contradiction or an absurdity, there is no possible model and that something does not exist.
Examples: (i) There is a rational number (fraction) which will measure the hypotenuse of an isosceles right triangle with a unit length for the side. (ii)There is a rational number (fraction) which will measure the side of the hypotenuse of a right triangle with a unit length for one side and a hypotenuse of length 2 units.
Proof starting with Euclid.
Proposition 1 Book 1
Euclid's tools. Proposition 1 and Proposition 2
Models for possibilities and impossibilities.
A model for the plane geometry of Euclid:
The basis for this model is understanding numbers!
Points: (a,b) where a and b are rational numbers.
Lines: Sets of points (x,y) that satisfy an equation Ax + By = C where A,B, and C are rational numbers and not all are 0.
Circles: Sets of points (x,y) that satisfy an equation of the form (x-A)2 + (y-B)2 = C where A,B, and C are rational numbers and C > 0.
Basic Facts: If I can build a model for the properties - the properties are consistent ( no contradictions or absurdities)
If I assume that something is possible (or exists) and arrive at a contradiction or an absurdity, there is no possible model and that something does not exist.
Examples: (i) There is a rational number (fraction) which will measure the hypotenuse of an isosceles right triangle with a unit length for the side. (ii)There is a rational number (fraction) which will measure the side of the hypotenuse of a right triangle with a unit length for one side and a hypotenuse of length 2 units.
