Thursday 3-10
Last class we applied Euler's
Formula for the plane or the sphere:
Theorem: For any connected graph in the
plane,
We'll continue to examine more applications of this topological property of graphs (networks) in the plane.
Counting Activity.
Last class we applied "Euler" to analysis of the Utilities problem and Complete graphs.
Coloring problems: Suppose we have a map that
consists of a graph that deteremines R regions ( countries) with E edges
(borders). How many colors are needed
to color the regions so that countries that share a border (not merely a
vertex) have different colors.
The
Junkyard on the color problem.
From Serendip
at Bryn Mawr College.
The Shockwave movie below makes it possible for you to play with the four
color problem yourself. Create a "map of countries" of any number, shape,
and size by drawing in the space, or let Serendip create a map for you by
clicking on the Generate Map button. The question is how many colors are
required to color such a map, using the rule that no two countries with adjacent
borders may be the same color (countries meeting at a point may be the same
color).
Once generated, either by you or by Serendip, click on Submit Map. After a processing delay, Serendip will then present the map to you in grey, and you can color individual countries by clicking on them (or let Serendip color the map for you). See if you can create a map that requires two colors, or three colors, or four colors. If you create one that requires five colors, you will upset mathematicians (and a few others) worldwide.Warning: Serendip has a small bug- so that sometimes it will give a less than best coloring of the map or will evaluate your work incorrectly.
Created by Paul Grobstein and Sasha Schwartz. Shockwave
programming by Sasha Schwartz. Reactions, comments, suggestions gratefully received.
Draw a map that needs 3 colors.
Draw a map that needs 4 colors.
Draw a map that needs 5 colors.
The Four Color Theorem: Any map on the plane or
the sphere can be colored with at most 4 colors.
The Color
problems: Discussion and proof of the five color theorem.
Some References for "proofs":
1995
summary of a new proof of the Four Color
Theorem and a four-coloring algorithm found by Neil Robertson,
Daniel P. Sanders,
Paul Seymour and Robin Thomas.
1999 article by Eric W. Weisstein © 1999 CRC Press LLC, © 1999-2003 Wolfram Research, Inc.
From the Math History web site: http://www-history.mcs.st-andrews.ac.uk/history/HistTopics/The_four_colour_theorem.html
Article by: J J O'Connor and E F Robertson JOC/EFR September 1996
However the final ideas necessary for the solution of the Four Colour Conjecture had been introduced before these last two results. Heesch in 1969 introduced the method of discharging. This consists of assigning to a vertex of degree i the charge 6-i. Now from Euler's formula we can deduce that the sum of the charges over all the vertices must be 12. A given set S of configurations can be proved unavoidable if for a triangulation T which does not contain a configuration in S we can redistribute the charges (without changing the total charge) so that no vertex ends up with a positive charge.
Heesch thought that the Four Colour Conjecture could be solved by considering a set of around 8900 configurations. There were difficulties with his approach since some of his configurations had a boundary of up to 18 edges and could not be tested for reducibility. The tests for reducibility used Kempe chain arguments but some configurations had obstacles to prevent reduction.
The year 1976 saw a complete solution to the Four Colour Conjecture when it was to become the Four Colour Theorem for the second, and last, time. The proof was achieved by Appel and Haken, basing their methods on reducibility using Kempe chains. They carried through the ideas of Heesch and eventually they constructed an unavoidable set with around 1500 configurations. They managed to keep the boundary ring size down to less than or equal to 14 making computations easier that for the Heesch case. There was a long period where they essentially used trial and error together with unbelievable intuition to modify their unavoidable set and their discharging procedure. Appel and Haken used 1200 hours of computer time to work through the details of the final proof. Koch assisted Appel and Haken with the computer calculations.
The Four Colour Theorem was the first major theorem to be proved using a computer, having a proof that could not be verified directly by other mathematicians. Despite some worries about this initially, independent verification soon convinced everyone that the Four Colour Theorem had finally been proved. Details of the proof appeared in two articles in 1977. Recent work has led to improvements in the algorithm.
Maps
Coordinates for "earth" - the sphere
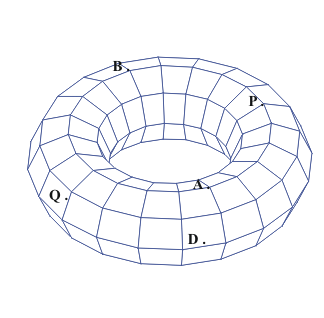
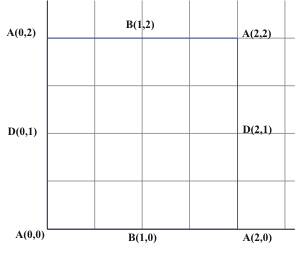
Coordinates for the torus!
Activity for maps on Torus.
Locate P and Q on the map! give their coordinates.
 |
 |
What is a surface?
Bounded, unbounded:
Closed, open:
With or without boundary:
Orientable or Non-orientable:
Can be realized (imbedded) in a plane, in 3 space, in 4 space.
Can be visualized (immersed) in ...
Examples:A closed disc, an open disc, a
plane, an annulus- cylinder, a mobius band;
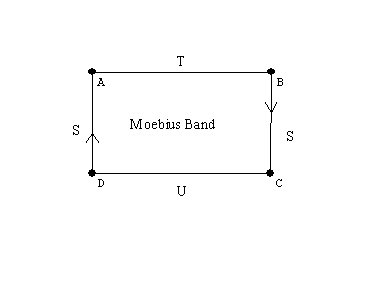
Experiments with the mobius band. Activity.
A sphere
A torus
[Activity:Graphs on the torus?]
The projective plane
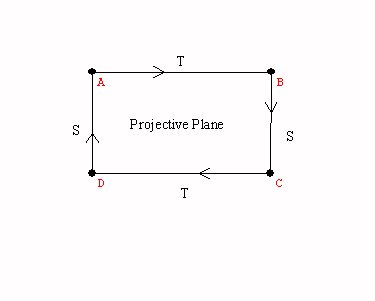
Spheres with handles:
Spheres with cross caps
Visualizations of surfaces by flattened
- cut apart models.
A cylinder, a mobius band, the torus, the Klein bottle, the projective plane.
Handles and cross-caps
attached to
the sphere.
The Topological Classification of "closed surfaces."