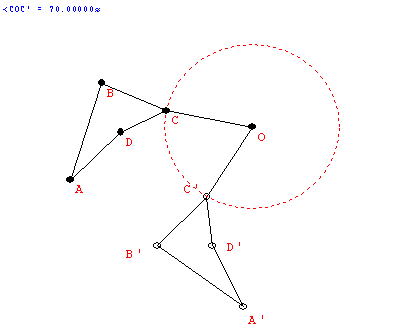
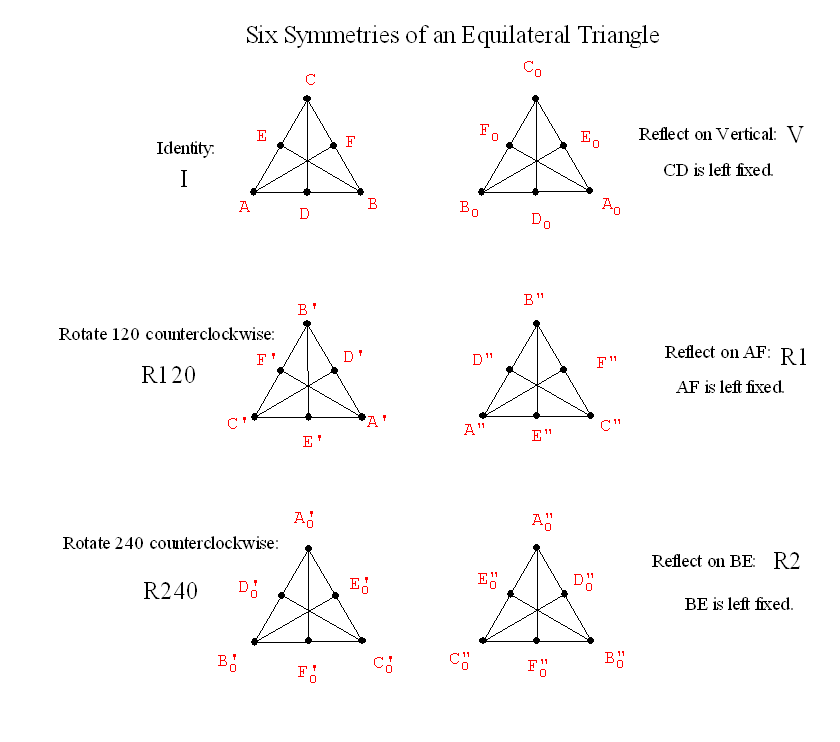
- The "flip."
- The "mirror."
-
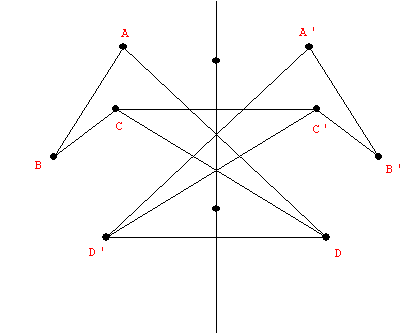
- R(P) = P' : A Transformation. Before: P .... After : P'
- If P is on the line (axis), then R(P)=P. "P remains fixed by the reflection."
- If P is not on the axis, then the line PP' is
perpendicular to the axis and if Q is the point of intersection of PP' with
the axis then m(PQ) = m(p'Q).
Squares... People