Monday, February 10, 2014
Class #6
- Example: Numbers for counting and measuring...
- numeral: a symbol for representing a number
- Number: a form of universal language to describe
anything/ physical things/ concepts related to
measurement
- Numerals : such as V, 5, five, cinq, chamesh,
cinco
- Frege distinguished numerals from numbers in the late
19th century.

- We can compare numbers... for instance we say"
3 is less than 5"
- Is 3 smaller than 5?
- Numerals are symbols (visual or linguistic) that we
use to represent numbers.
- Numbers are concepts. They are not physical objects but are used to
describe a quality of an object or a collection of objects. Some regard
numbers as abstract entities that "exist" in a non-physical world -
sometimes described a "platonic" after the Greek philosopher Plato.
- We use numbers to measure (lengths) and put things
in order (which was first).
- Another common visual representation of numbers uses
the number line.
- ___.___.___.___.___.___.___.______
-
1 2
3 4
5 6 7
Here the numerals are associated with points, so "the points
visualize the corresponding numbers."
Geometric Puzzle Foundations
- Measuring angles, lengths and areas.
- Triangles
: add to 180 degrees- straight angle [Illustrate physically and with Wingeometry andGeoGebra]
- Squares, rectangles : 90 degree/ right
angle
More on measurements of angles of polygons with n sides. .
When n = 3 this is a triangle, n=4, a quadrilateral, or
when n= 5, a pentagon.

The sum of the measures of the
interior angles of a triangle is 180 degrees.
What about a quadrilateral? and a pentagon?
or an n sided polygon ( an "n -gon")?
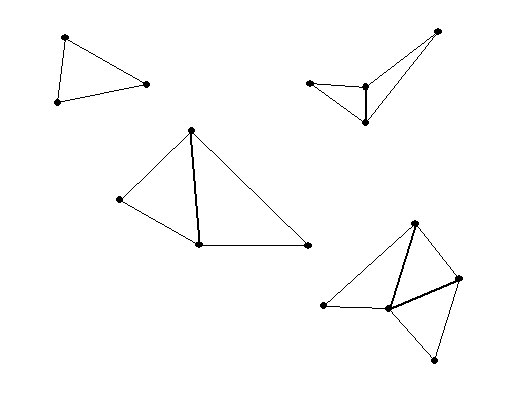
- A quadrilateral can be made from two triangles...
so the sum of its interior angles is 2 * 180 = 360. - A pentagon can be made from 3 triangles...
so the sum of its interior angles is 3* 180 = 540. If the pentagon has
all angles congruent( of equal measurement) then each angle will be 540/5
= 108 degrees!
- A hexagon can be made from 4 triangles...
so the sum of its interior angles is 4* 180 = 720. If the hexagon has all
angles congruent( of equal measurement) then each angle will be 720/6 =
120 degrees!
- One polygonal Tile: Quadrilateral Activity.
- Use 4 identical convex quadrilaterals to surround a single vertex. Find a way to do this that can be extended to tile the plane:
- It was demonstrated with wingeometry how to do this with a non-convex quadrilateral:
-

