Recall Symmetries of an equilateral triangle:
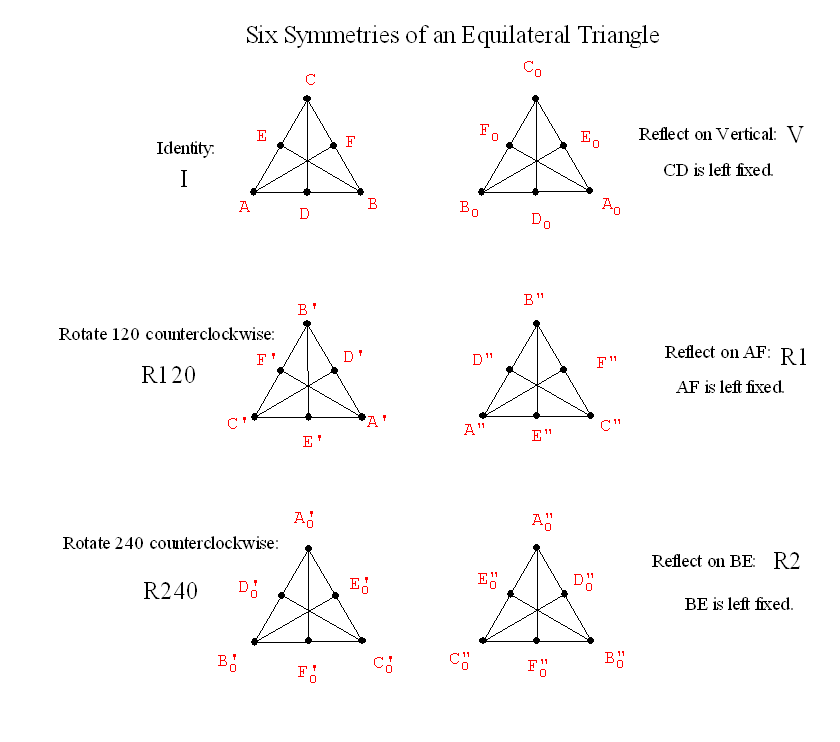


| * |
Id |
R120 |
R240 |
V |
G=R1 |
H=R2 |
| Id |
I |
|||||
| R120 |
R240 |
R1 |
||||
| R240 |
I |
R2 |
||||
| V |
R2 |
R1 |
I |
R120 |
||
| G=R1 |
I |
|||||
| H=R2 |
I |
|
translation |
horizontal |
vertical |
|
reflection + |
glide |
rotation |
reflection + |

 translations |
 reflections |

reflections + |

glide |

reflections + |
 rotations (2) |

reflections + |

rotations (2) + |

rotations (2) + |
 rotations (4) |

reflections + |

rotations (4) + |
 rotations (3) |

reflections + |

rotations (3) + |
 rotations (6) |

reflections + |
Classification of IsometriesRigid Motions in (or about) the plane. Also called "Isometries" Orientation preserving Translations Rotations Orientation reversing Reflections Glide reflections
Next Class...Video : Isometries
The video introduced the four isometries we have discussed:
reflections, rotations, translations, and glide reflections.
It was shown that the product of two reflections is either a rotation (if the axes of the reflection intersect) or a translation (if the axes of the reflection are parallel).
Wingeometry demonstration for reflection- one and two reflections
What about 3 reflections? How to figure out.... match features.
Every plane isometry is the product of at most three reflections.
Two reflections = rotation or translation.Three reflections = reflection or glide reflection
Preserve
OrientationReverse
OrientationNo Fixed points Translation Glide reflection Fixed Point(s) Rotation Reflection Using Isometries to recognize symmetries of a figure or tiling.