- Measurement and the Pythagorean Theorem (PT) [1.1]
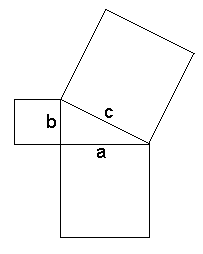
a2 + b2 = c2
How can one distinguish the
sphere from a plane (Flatland) based solely on experiences
on the surface?
How can one distinguish the
sphere from a torus based solely on experiences on the surface?
Use shadows?: look at shadows at the same time of
day? This is a "local" feature of the surface.
Observe "curvature"? This is also a local property.
Circumnavigate (Global)?: Go West -> return
from the East, then go North-> return from the south.
On a sphere: there will always be 2 points of intersection
of the curves determined by the two routes.
On a torus: There will be only one point of intersection
of the two routes.
plane: Go West -> you keep going... there seems
to be no return???
Other issues: What about strange gravity? Finding an edge? How do you know
when you start?
From Wikipedia, the free encyclopedia.
The halting problem is a decision problem which can be informally
stated as follows:
Given a description of an algorithm and a description of its initial arguments, determine whether the algorithm, when executed with these arguments, ever halts (the alternative is that it runs forever without halting).
Alan Turing proved in 1936 that there is no general method or algorithm which can solve the halting problem for all possible inputs.
The importance of the halting problem lies in the fact
that it was the first problem to be proved undecidable. Subsequently, many
other such problems have been described; the typical method of proving a
problem to be undecidable is to reduce it to the halting problem.

Show video on PT- Put on reserve in library!
Background: Similar triangles
Area of triangles = 1/2 bh
Area of parallelogram= bh
Scaling: a linear scale change of r gives area change of factor r^2.
3 questions: running, moat, wind power...
Proof of the PT: Similar right triangles c = a^2/c + b^2/c.
applications and other proofs.
Prop. 47 of Euclid.
Dissection Proof.
Prop 31 Book VI Similar shapes.
Simple proof of PT using similar triangles of the triangle.
Use in 3 dimensional space.