Thursday, January 20 (ppt)

---

• More Introduction to course organization.
• Web Materials
• What is Visual Mathematics?
• Mathematics that studies topics related to visual experience. [Geometry, Topology, Motion]
  
• Visualization of mathematics that is not inherently visual. [Visualizing Counting] 
• Example: Numbers...
  
• numeral: a symbol for representing a number 
• Number: a form of universal language to describe anything/ physical things/ concepts related to measurement
• 
  
• such as V, 5, five, cinq, chamesh, cinco
• Frege distinguished numerals from numbers in the late 19th century.
• We can compare numbers... for instance we say" 3 is less than 5"
• Is 3 smaller than 5?
• Numerals are symbols (visual or linguistic) that we use to represent numbers.
• We use numbers to measure (lengths) and put things in order (which was first).
• Another common visual representaion of numbers uses the number line.
• ___.___.___.___.___.___.___.______
•       1     2     3     4     5     6     7

Here there numerals are connected to points, so the points are considered to visualize the corresponding numbers.

Use Wingeometry?

• We visualize equations that  give relations between numbers with graphs in the coordinate plane.

3x + 2y = 6 is visualized by the graph of a line ... Use Wingeometry? or Winplot?
• Another example of "visual Math":
• My Name: Martin Flashman
• How to start a letter to me:  Hello ___________
  

Professor	Martin
Doctor	Marty	Flashman
Mister	Flash	omit
Omit	Omit

• How many different openings are possible?
  
• We can visualize this problem with a "tree"
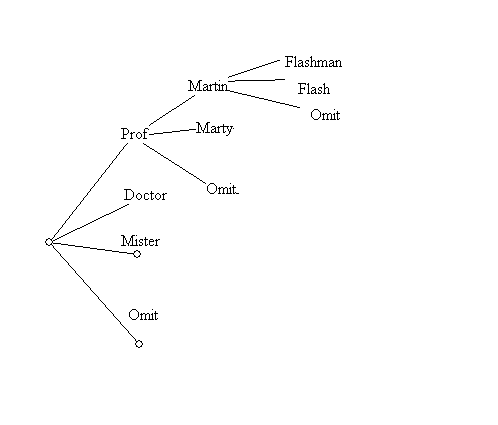
• This visualization allows us to count the possibilities easily...

seeing there are 8 possibilities for each of 4 title branches
so that the total is 8*4 = 32 possibilities.
• This is an example of a visualization used to understand and solve a problem that initially is not connected to anything visual .
• Miscellaneous: Some topics we will study.
• The film lists as a guide to the course topics.
• The color problem.
• The motion problem.
  
• The Sphere  and the Torus.

Who first showed the earth was a sphere?

---

• Measurement and the Pythagorean Theorem (PT) 

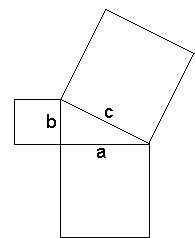
a² + b² = c²




• Measuring angles, lengths and areas.
• Squares, rectangles, parallelograms and triangles.
• Dissections, cut and paste methods of measurement.
• Cutting and reassembling polygons.
• The Square Me Puzzle.
• Do Pythagorean Activity Sheet
• Virtual Manipulative for PT.
• Discuss Pythagorean Theorem and proofs.
• Over 30 proofs of the Pythagorean theorem!
• Many Java Applets that visualize proofs of the Pythagorean Theorem

---

• Show video on PT
• Puzzles and Polygons
  
• Flatland and the plane
• The triangle, quadrilateral, pentagon, and hexagon.
• More on measurements of angles and areas of polyons.
• Activity: Measuring angles in regular polygons.