Last class we started  a discussion of

Surfaces:Mark Sudduth's web page of surfaces.[ A physics master's degree student at UT, Arlington.

What is a surface?
Bounded, unbounded:
Closed, open:
With or without boundary:
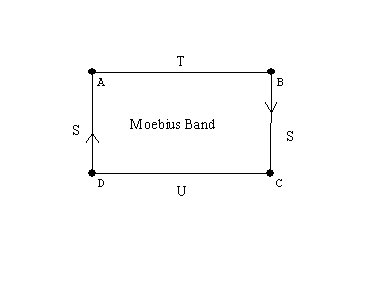
Orientable or Non-orientable: we considered the moebius band and the Klein Bottle as examples of non-orientable surfaces.
Can be realized (imbedded) in a plane, in 3 space, in 4 space.
Can be visualized (immersed) in ...


Examples:A closed disc, an open disc, a plane, an annulus- cylinder, a mobius band;

 

Experiments with the mobius band. Drawing a curve along the center of the band we cover both "sides." Cutting along that curve the band does not fall apart, but gets twice as long!

a sphere,
a torus

 

a Klein bottle

,

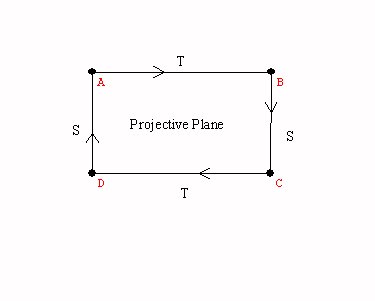
the projective plane... Why is this a closed and bounded surface?

;

A sphere with a cross cap .

Activity:Graphs on the torus.
Games and puzzles on the torus and the klein bottle.

Visualizations of surfaces by flattened - cut apart models.
A cylinder, a mobius band, the torus, the Klein bottle, the projective plane.


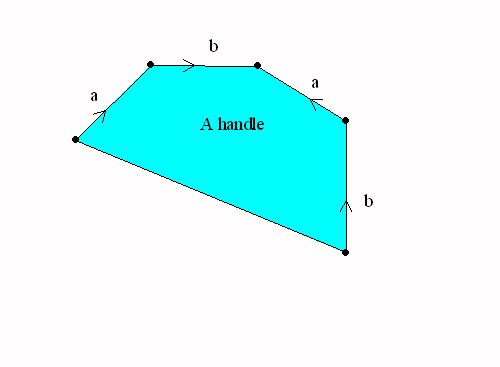
Closed Surfaces: Handles and cross-caps  attached to the sphere.

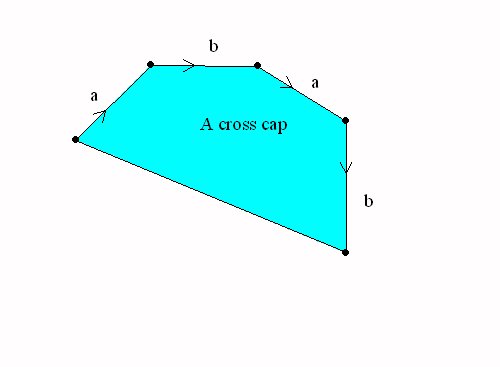
A sphere with a handle = a torus	A Sphere with a cross cap = the projective plane

The Topological Classification of "closed surfaces."

Every connected closed and bounded surface is topologically equivalent to a sphere with handles and crosscaps attached.


Proof....

This classification determines the euler characteristic of each surface.
If the surface is orientable, it is a sphere with n handles, so V-E+R = 1 - 2n +1 = 2-2n.  For example the torus has euler characteristic 2-2*1=0.
If the surface is non-orientable, then  is it a sphere with k crosscaps and n handles, so the euler characteristic is V-E+R = 1 - (k+2n) +1 =2 -2n -k.
Notice that a sphere with two cross caps has euler characteristic 0, the same as the torus. But this was the euler characteristic of the Klein Bottle. So we should be able to recognize the Klein bottle as a sphere with two cross caps.
This can be done by a single normalization of one pair of edges with the same  orientation.

---

Other interest in surfaces: Examples
Ways to think of surfaces : cross-sections/ projections/moving curves/ using color to see another dimension.

Generalization of surfaces are called "manifolds".  cross sections / projections/ moving surfaces-solids.
"minimal surfaces" (FAPP video?)
Transforming surfaces: "turning the sphere inside out." video

---