Last class we started a discussion of
Surfaces:Mark Sudduth's web page of surfaces.[ A physics master's degree student at UT, Arlington.
What is a surface?
Bounded, unbounded:
Closed, open:
With or without boundary:
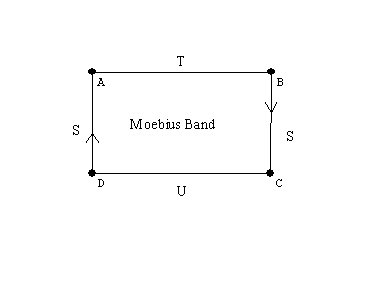
Orientable or Non-orientable: we considered the moebius band and the Klein Bottle as examples of non-orientable surfaces.
Can be realized (imbedded) in a plane, in 3 space, in 4 space.
Can be visualized (immersed) in ...
Examples:A closed disc, an open disc, a
plane, an annulus- cylinder, a mobius band;

Experiments with the mobius band. Drawing a curve along the center of the band we cover both "sides." Cutting along that curve the band does not fall apart, but gets twice as long!
a sphere,
a torus
a Klein bottle
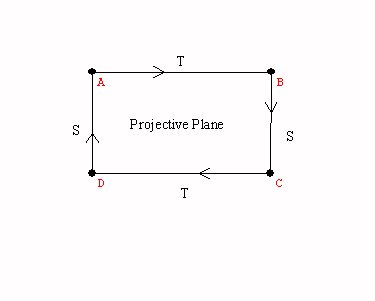
the projective plane... Why is this a closed and bounded surface?
Activity:Graphs on the torus.
Games and puzzles on the torus and the klein bottle.
Visualizations of surfaces by flattened
- cut apart models.
A cylinder, a mobius band, the torus, the Klein bottle, the projective plane.
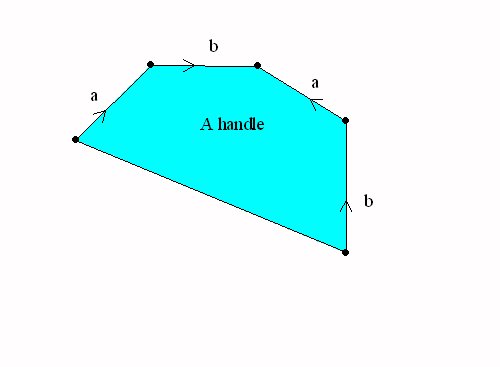
Closed Surfaces: Handles and cross-caps attached to the sphere.
|
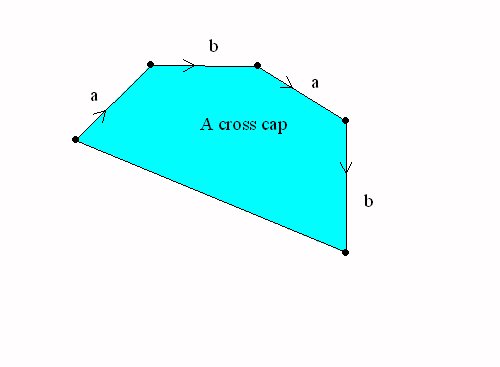
|

A sphere with a handle = a torus |

A Sphere with a cross cap = the projective plane |
The Topological Classification of "closed surfaces."
Every connected closed and bounded surface is topologically equivalent to a sphere with handles and crosscaps attached.