
Presentations of Student Projects.
Final grades will be submitted by Friday 12-19.
Projects and portfolios may be recovered on 12-19 or at the beginning of Spring term.
At the end of class, 3:05 pm, there will be time for a course evaluation.
Your comments and suggestions related to Math 103 are welcome.
You can send them to me directly by E-Mail: flashman@humboldt.edu
Last class we continued the discussion of
Surfaces:
a sphere
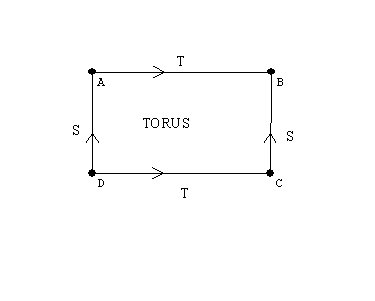
a torus
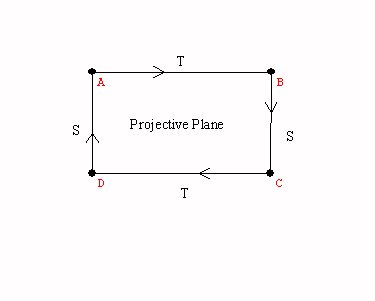
a Klein bottle
the projective plane... The euclidean plane with the horizon line.
Why is this a closed and bounded surface?
Response:
Each point in the ordinary plane corresponds to a point on the upper hemisphere.
An ideal point on the horizon will correspond to two points on the equator.
These two points need to be identified to give a one point for one point
correspondence of this representation of the projective plane. [download winplot file]

Visualizations of surfaces by flattened
- cut apart models.
A cylinder, a mobius band, the torus, the Klein bottle, the projective plane.
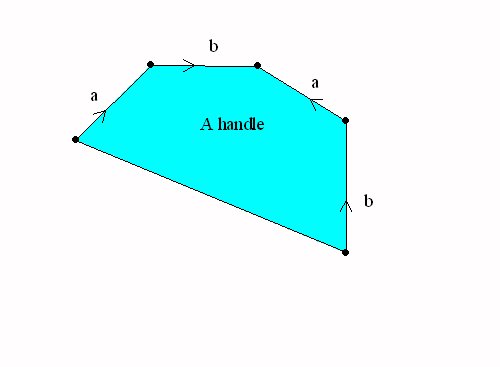
Closed Surfaces: Handles and cross-caps attached to the sphere.
|
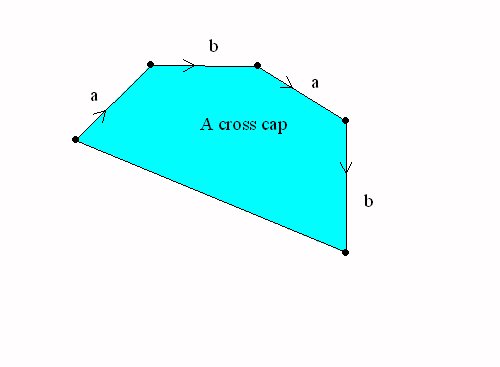
|

A sphere with a handle = a torus |

A Sphere with a cross cap = the projective plane |
The Topological Classification of "closed surfaces."
Every connected closed and bounded surface is topologically equivalent to a sphere with handles and crosscaps attached.
From the Fun Fact files,
hosted by the
Harvey Mudd College Math Department , Unbelievable Unlinking
Imagine that the two objects in Figure 1 are solid (with thickness) and made of very flexible and stretchy rubber. Question: is it possible to deform one object into the other in a continuous motion (without tearing or cutting)? Surprise answer: Yes!! Hint: it is important that the object is solid and has thickness; this transformation cannot be done with a one-dimensional piece of string. It is also not possible to do this with a piece of rope because even though the rope has thickness, it is not flexible or "stretchy" enough. See below for an explanation and animated gif. Or, don't scroll down if you want to think about it a while! The Math Behind the Fact: Graeme McRae has generously contributed the
animated gif in Figure 2, showing another solution to
this problem! (Thank you, Graeme!) |