
Curves and Surfaces:What is possible? what
is not?
What is the difference between Euclidean Geometry, Projective Geometry,
and "Topology"
Euclid: congruence, similar... measurements,
scale Questions: Is a triangle congruent/similar to another triangle?
Is an ellipse congruent /similar to a parabola?
Is a triangle congruent/similar to a square?
Projective: perspectivity, projectivity,
lines, points of intersection and contact (tangency).
Questions: Is a triangle
projectively related to another triangle?
Is an ellipse projectively related to a parabola?
Is a triangle projectively
related to a square?
Topology:
"Bounded" In the plane- A line segment is bounded. A line is not bounded.
A circle is bounded. A parabola is not bounded. "Bounded" means the
object can be visualized in a box.
"closed" A line segment with endpoints is closed. A circle is closed.
A line is closed. A line segment missing one or both endpoints in not closed.
A circle missing one point is not closed.
"open" A line segment missing both endpoints is open. A line is open.
A circle missing one
point is open.
"connected" A line, a line segment, a circle, a circle missing one point,
and a parabola are all connected.
A line segment missing an interior point is not connected.
It has two pieces.
The following two letters are topologically equivalent. The following two letters are topologically equivalent.
I C
The following two letters are topologically equivalent to each other but not to the previous two letters.
This can be seen by removing a single point from these letters which will
not disconnect the curves, as it does with the previous letters.
O D
The letter T missing the point
where the top meets the vertical line segment is not connected. It has three
pieces.
The letter Y missing the point where the top meets
the vertical line segment also is not connected. It has three pieces.
T and Y are
topologically the same! this can be seen by bending the tops to the letters
up or down and stretching and shrinling the lengths as well.
Questions: Is a triangle
topologically related to another triangle?
Yes. stretch the sides and you'll also rasnform the angles.
Is an ellipse topologically
related to a parabola?
No.
The ellipse is bounded and still connected when you remove a point.
The parabola is not bounded and is disconnected when you remove a point.
Is a triangle topologically
related to a square?a circle? yes.
Topology: Counting on a line. Counting
on a curve.
Keep count on the number of vertices and segments for a graph.
Compare:
| Vertices |
Edges |
V-E |
|
| Line segment | 2 |
1 |
1 |
| circle | 1 |
1 |
0 |
| 8 | 1 |
2 |
-1 |
| 9 | 2 |
2 |
0 |
| B | 2 |
3 |
-1 |
Curves will not be topologically
equivalent if the number V-E is not the same. However, as the table shows,
there are curves that have the same number V-E which are also not equivalent.
These can be distinguished by other criterion, such as connectivity when
a point is removed.
The number V-E is a characteristic of the curve that will be the same for
any topologically equivalent curve. However, this number does not completely
classify the curves topologically, since curves can the same number V-E without
being equivalent.
Counting in the plane or Counting on a
surface.
Vertices, edges, regions.
| Vertices |
Regions | Edges | |
| Line segment | 2 |
1 |
1 |
| circle | 1 |
2 |
1 |
| 8 | 1 |
3 |
2 |
| 9 | 2 |
2 |
2 |
| B | 2 |
3 |
3 |

|
6 |
8 |
12 |
Counting in the plane or Counting on a
sphere.
Euler's Formula for the plane
or the sphere:
Theorem: For any connected graph in the plane, V+R = E + 2.
OR V -E+R =2 The number 2 is called the "Euler characteristic
for the plane." ( and the sphere).
Proof: Deconstruct the graph.
First remove edges to "connect regions" until there is only one region.
The relation between V+R and E+ 2 stays the same. (One edge goes with
one region.)
Now remove one vertex and edge to "trim the tree". Again the relation between
V+R and E+2 stays the same. ( One edge goes with each vertex.) Finally
we have just one vertex, no edges, and one region. So the relationship
is that V+R = E + 2!
For any connected graph on the sphere, V+R = E + 2
Proof: Choose a point P on the sphere not on
the graph. Place a plane touching the sphere opposite to P. Then project
the graph onto the plane. The projected graph will have the same number of
vertices, edges and regions. The counting in the plane shows that the formula
is true for the projected graph, and thus for the original graph on the sphere!
What about graphs on the Torus?
We have a connected graph on the torus with one vertex, two edges and only
on region. But this information does not match for the euler formula for
the plane or the sphere. SO.. the torus must be topologically different from
the sphere or the plane!
In fact for the torus we see that it is possible for V+R= E or V-E+R=
0
In our last class we discussed counting in the plane or counting on a sphere.
We learned about (and proved) Euler's Formula for the plane or the sphere:
Here are some applications of this topological property of graphs:
The Utilities problem:
There are three houses being planned on a new development owned by Aron(A),
Beth(B), and Carol (C). The phone company(P), cable company(L), and electric
company(E) are planning to put in underground lines to the three houses and
to minimize interference between the services, they would like to set up
separate lines from there connection boxes to the houses that do not cross
on the map of the development.
Draw a design the will achieve this objective.
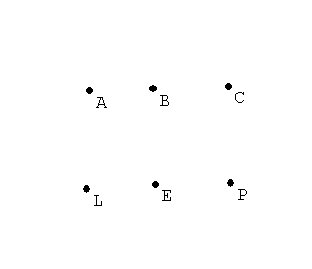
Discussion: Analysis. Suppose this were possible and consider the consequences.
If the graph were drawn it would have ____ E=9___ edges.
Based on Euler's formula, the graph would therefore have to have _____R=5___
regions in the plane.
by design each region would have to have at least 4 edges. Thus if we count
the edges by the regions we would have at least 4R edges counting each edge
twice- because an edge is a boundary for exactly two regions. Thus the number
of edges must be more than 2R.
Is this possible? What can we conclude?
Complete graphs. A complete graph is a graph in which each vertex of the graph is connected by an edge to every other vertex.
For example:
2 vertices: 1 edge - a line segment
3 vertices: 3 edges - a triangle
4 vertices: 6 edges - a tetrahedron
Notice these all have planar representations.
What about 5 vertices?
Draw a complete graph using 5 vertices.
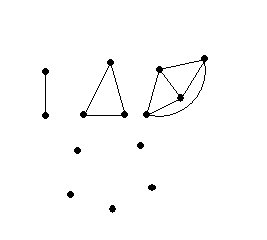
Discussion: Analysis. Suppose this were possible and consider the consequences.
If the graph were drawn it would have ____ E=10___ edges.
Based on Euler's formula, the graph would therefore have to have _____R=7___ regions in the plane.
by design each region would have to have at least 3 edges. Thus if we count
the edges by the regions we would have at least 3R=21 edges counting each edge
twice- because an edge is a boundary for exactly two regions. Thus the number
of edges must be more than 3/2R=10 1/2.
Is this possible? What can we conclude?
Coloring problems: Suppose we have a map that
consists of a graph that deteremines R regions ( countries) with E edges
(borders). How many colors are needed to color the regions so that countries that share a border (not merely a vertex) have different colors.
The Junkyard on the color problem.
From Serendip at Bryn Mawr College.
The Shockwave movie below makes it possible for you to play with the
four color problem yourself. Create a "map of countries" of any number,
shape, and size by drawing in the space, or let Serendip create a map for
you by clicking on the Generate Map button. The question is how many colors
are required to color such a map, using the rule that no two countries with
adjacent borders may be the same color (countries meeting at a point may
be the same color).
Once generated, either by you or by Serendip, click on Submit Map. After a processing delay, Serendip will then present the map to you in grey, and you can color individual countries by clicking on them (or let Serendip color the map for you). See if you can create a map that requires two colors, or three colors, or four colors. If you create one that requires five colors, you will upset mathematicians (and a few others) worldwide.Warning: Serendip has a small bug- so that sometimes it will give a less than best coloring of the map or will evaluate your work incorrectly.
Created by Paul Grobstein and Sasha Schwartz. Shockwave programming by Sasha Schwartz. Reactions, comments, suggestions gratefully received.
Draw a map that needs 3 colors.
Draw a map that needs 4 colors.
Draw a map that needs 5 colors.
The Four Color Theorem: Any map on the plane or the sphere can be colored with at most 4 colors.
The
Color problems: Discussion and proof of the five color theorem.
Some References for "proofs":
1995 summary of a new proof of the Four Color
Theorem and a four-coloring algorithm found by
Neil Robertson,
Daniel P. Sanders,
Paul Seymour and
Robin Thomas.
1999
article by Eric W. Weisstein
© 1999 CRC Press LLC,
© 1999-2003 Wolfram Research, Inc.
From the Math History web site: http://www-history.mcs.st-andrews.ac.uk/history/HistTopics/The_four_colour_theorem.html
Article by: J J O'Connor and E F Robertson JOC/EFR September 1996
However the final ideas necessary for the solution of the Four Colour Conjecture had been introduced before these last two results. Heesch in 1969 introduced the method of discharging. This consists of assigning to a vertex of degree i the charge 6-i. Now from Euler's formula we can deduce that the sum of the charges over all the vertices must be 12. A given set S of configurations can be proved unavoidable if for a triangulation T which does not contain a configuration in S we can redistribute the charges (without changing the total charge) so that no vertex ends up with a positive charge.
Heesch thought that the Four Colour Conjecture could be solved by considering a set of around 8900 configurations. There were difficulties with his approach since some of his configurations had a boundary of up to 18 edges and could not be tested for reducibility. The tests for reducibility used Kempe chain arguments but some configurations had obstacles to prevent reduction.
The year 1976 saw a complete solution to the Four Colour Conjecture when it was to become the Four Colour Theorem for the second, and last, time. The proof was achieved by Appel and Haken, basing their methods on reducibility using Kempe chains. They carried through the ideas of Heesch and eventually they constructed an unavoidable set with around 1500 configurations. They managed to keep the boundary ring size down to less than or equal to 14 making computations easier that for the Heesch case. There was a long period where they essentially used trial and error together with unbelievable intuition to modify their unavoidable set and their discharging procedure. Appel and Haken used 1200 hours of computer time to work through the details of the final proof. Koch assisted Appel and Haken with the computer calculations.
The Four Colour Theorem was the first major theorem to be proved using a computer, having a proof that could not be verified directly by other mathematicians. Despite some worries about this initially, independent verification soon convinced everyone that the Four Colour Theorem had finally been proved. Details of the proof appeared in two articles in 1977. Recent work has led to improvements in the algorithm.