Step 5. Normalize pairs A.... A with opposite orientation.
Consider the edges between A and A.
If every edge between the heads of A is paired with an edge also between the heads of A, then no vertex between the heads of A can be identified with a vertex between the tails of A. BUT this can't be, since all the vertices are the same.
So... there must be at least one pair of edges R, with opposite orrientations with one between the heads and the between the tails of A.

Then cut from the head of C (opp) to the head of R with an edge S.
Now cut between the heads of the R's with an edge C  | and paste the A's together.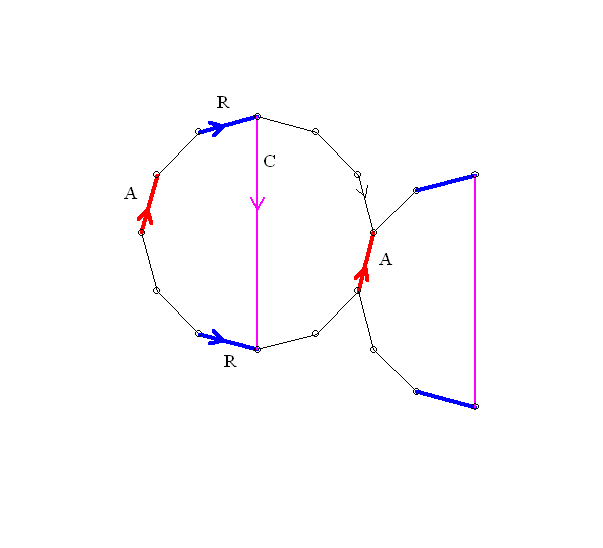 | This gives .... RCR(opp).....C(opp)... [The A's are now inside the polygon.] 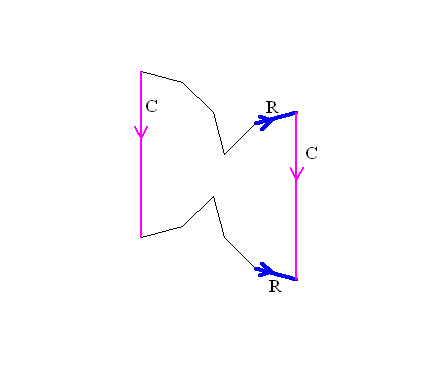 |

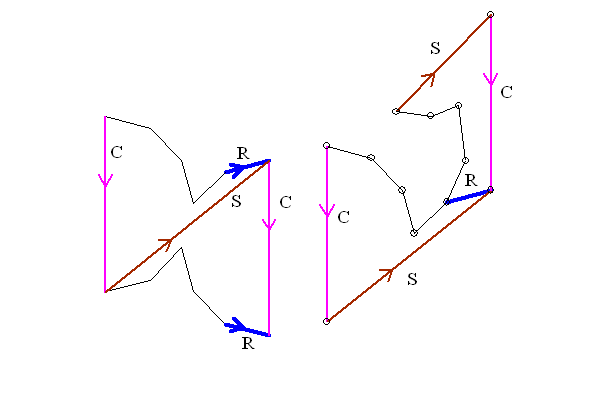
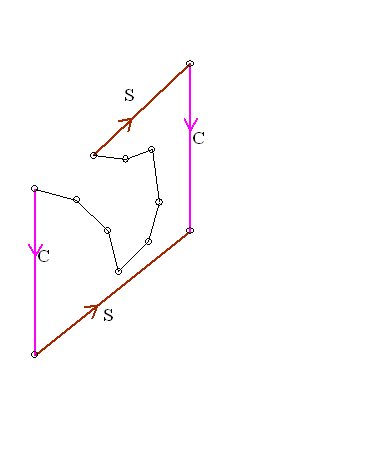
Continue with this normalization until all edges have been normalized.
Conclusion: (1) If there were no step 4 pairs, then you have a sphere with as many handles to give the appropriate number of edges. [ n handles -> 2n edges.]
(2) If there were k - step 4 pairs and n step 5 quadruples, then you have a sphere with k crosscaps and n handles and k +2n edges.
This classification determines the euler characteristic of each surface.
If the surface is orientable, it is a sphere with n handles, so V-E+R = 1 - 2n +1 = 2-2n.
For example, the torus has euler characteristic 2-2*1=0.
If the surface is non-orientable, then it is a sphere with k crosscaps and n handles, so the euler characteristic is V-E+R = 1 - (k+2n) +1 =2 -2n -k.
Notice that a sphere with two cross caps has euler characteristic 0, the same as the torus. But this was the euler characteristic of the Klein Bottle. So we should be able to recognize the Klein bottle as a sphere with two cross caps.
This can be done by a single normalization of one pair of edges with the same orientation.