Proposition:
(i) The product of two reflections that have the lines of reflection intersect at a point O is a rotation with center O through an angle twice the size of the angle between the two lines of reflection.
(ii) The product of two reflections that have parallel lines of reflection is a translation in the direction perpendicular to the two lines and by a length twice the distance between the two lines of reflection.
(iii)The product of three reflections is either a reflection or a glide reflection.
Proof: We can do this geometrically or using the matrices!
Geometric Proof:(outline)
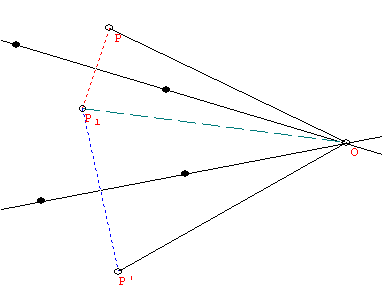
(i) and (ii): Suppose S and T are the reflections and P' = ST(P) for any point P.
For (i): Recall that O denotes the point of intersection of the lines of reflection of S and T.
It suffices to show that PO is congruent to P'O and that <POP' is congruent to the double of the angle between the lines of reflection.
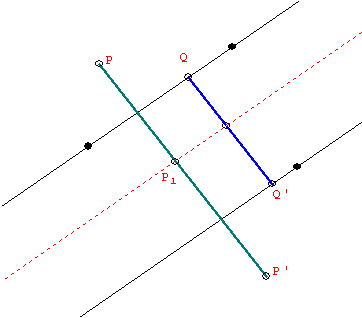
For (ii) It suffices to show that PP' is perpendicular to both lines of reflection and that if QQ' is a line segment with Q on one reflection line and Q' on the other and QQ" perpendicular to the line, then PP' is congruent to the double of QQ'.
For (iii)
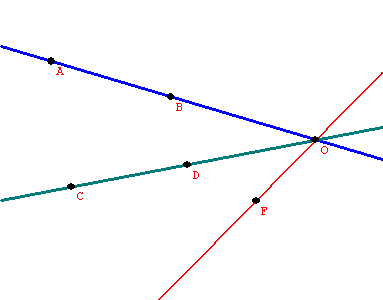
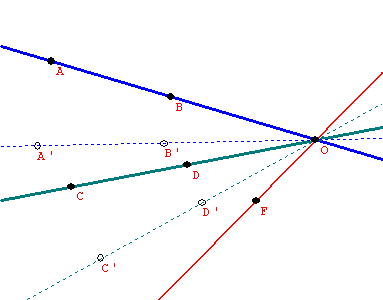
(a)Suppose all three lines have a point in common, O.
Holding the angle between the first and second lines of reflection fixed, rotate the pair about the point O until the second line coincides with the third line of reflection.
So the product on the three lines is the same as the reflection on the rotated first line.
 |
 |
(b) Suppose no pair of the three line is parallel but they have no single point in common.
So the three lines form a triangle.
Rotate the first and second lines with the angle between them held fixed on their common point
until the second line is perpendicular to the third line.
Now rotate the second and third lines about the point where they now intersect at a right angle
until the third line is perpendicular to the first line.
So the transformed first and second lines are now parallel
and the translation determined by the product of these reflections is parallel to the third line,
so the product of the three reflections is a glide reflection.
(c) Suppose the three lines form a pair of parallel lines with a transverse line. Then rotate the transverse line and one of the parallels with which it is composed, holding the angle between them fixed about the point of their intersection, so that the three resulting lines are organized as in b. Thus this product is also a glide reflection.
(d) Suppose all three lines are parallel. Holding the distance between the first and second lines of reflection fixed, we translate the pair by a vector perpendicular to them both until the second line coincides with the third line of reflection. So the product on the three lines is the same as the reflection on the first line (translated).
EOP
Algebraic proofs of (i) and (ii):
(i) Assume that the point of interection of the two lines is the origin and the first line of reflection is the X Axis , while the second line has equation AX +BY =0. So, ST(x,y) = S (x, -y) = ?
Suppose the line makes an angle t with the X-axis. Then
(ii) Assume the first line is the X axis and the second line has equation Y = c. Then
ST(x,y) = S (x,-y) = (x, -y + 2(c+y) ) = (x, y +2c)
But if W is vertical translation by 2c, then W(x,y) = (x,y+2c).
So ST(x,y) = W(x,y).
(i) Assume that the point of interection of the two lines is the origin and the first line of reflection is the X Axis , while the second line has equation AX +BY =0. So, ST(x,y) = S (x, -y) = ?
Suppose the line makes an angle t with the X-axis. Then
ST(x,y) = S(x,-y) = Rt RX R-t (x,-y)
=Rt RX ( cos(-t)x+ -sin(-t)(-y), sin(-t) (x) + cos(-t) (-y))
=Rt RX (x cos(t) - ysin(t), -xsin(t) - ycos(t))
=Rt (x cos(t) - ysin(t), xsin(t) + ycos(t))
= (cos(t)[x cos(t) - ysin(t)] + -sin(t)[ xsin(t) + ycos(t)], sin(t)[x cos(t) - ysin(t)] + cos(t)[ xsin(t) + ycos(t)])
= (x cos2(t) - ycos(t)sin(t) - xsin2(t) - ysin(t)cos(t), x sin(t) cos(t) - ysin2(t) + xcos(t)sin(t) + ycos2(t))
= (x cos(2t)) - ysin(2t) ,x sin(2t) + ycos(2t))
= R2t (x,y)
(ii) Assume the first line is the X axis and the second line has equation Y = c. Then
ST(x,y) = S (x,-y) = (x, -y + 2(c+y) ) = (x, y +2c)
But if W is vertical translation by 2c, then W(x,y) = (x,y+2c).
So ST(x,y) = W(x,y).