Martin Flashman
Department of Mathematics
Humboldt State University
Mathematics Beyond Good and Evil:

in Geometry, Algebra, and Calculus!
Work in Progress
Thursday, November 21





3 points - 3 lines. |

N points - N lines. |
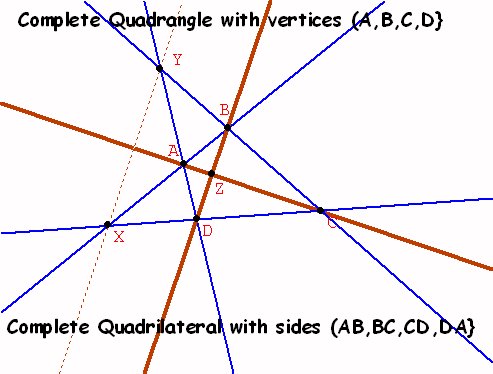 4 points {A,B,C,D} determine 6 lines {AB,AC,AD, BC, BD, CD} and three additional points {X,Y,Z}. |

The Complete Quadilateral: 4 lines {AB, BC, CD,AD}determine 6 points {A,B, C, D, X,Y} with three additional lines{AC, BD, XY} . |


|
|
|
|
from a point |
from a line |
Desargue's Spatial Configuration

Pascal: 9 points - 7 lines A Point Conic |

Brianchon: 9 lines - 7 points A Line Conic |
Between neighboring regions add an edge crossing the original
border connecting the dual vertices.
Every capital has a highway directly connecting it to neighboring capital.
Every vertex will be surrounded by a network of dual edges enclosing it in a dual region.
The dual map is made up of the dual vertices, dual edges
, and the resulting dual regions.

Map in black. Dual Map in red. |

|
This would have five vertices and each vertex would be connected to every other vertex by an edge ... a complete graph on 5 vertices.
But this graph would have 5 vertices and 10 edges and by Euler's formula* (Not proven here!) that
Thus there must be 7 regions, and
each region would have at least 3 edges.
So if we count the edges (twice - once for each region
on the edge) we would have at least 21 "edges" or at least 11 edges
without double counting.
Which is a contradiction, since there are just 10
edges.
Here is a table showing the five platonic solids and the
duality relation of Vertices, Edges, and Faces:
|
|
V |
|
|
|
|
8 |
|
|
|
|
6 |
|
|
|
|
12 |
|
|
|
|
20 |
|
|
|
|
|
|
|
Primal linear program problem: Min{cx:
x >= 0, Ax >= b}.
Example: Minimize: C = x + 2y
5x + 7y >= 4
3x + 8y >= 3
Dual linear program problem:
Max{yb: y >= 0, yA <= c}.
Dual Example: Maximize: P = 4x + 3y
5x + 3y <= 1
7x + 8y <= 2
Gale, Kuhn and Tucker (1951) proved the fundamental strong
duality theorem:
Duality Theorem of Linear
Programming.
For an LP primal-dual pair,
exactly one of the following holds:
1. The primal has
an optimal solution, in which case so must the dual, and their objective
values are equal.
2. The primal is infeasible, in which case the dual is either infeasible or unbounded.
3. The primal is
unbounded, in which case the dual is infeasible.
We'll call [A,B,C] homogeneous coordinates of the P-line.
For example, [1,0,1] are homogeneous coordinates
for the P-line determined by the plane with equation X + Z = 0.
For example, <1,0,-1> are homogeneous coordinates
for the P-point determined by the line with equation (X,Y,Z) = (1,0,-1)
t.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Point | Interval |
| Static | Dynamic |
| Evaluation
Form
ò abf (x) dx = F(b) - F(a) |
Derivative
Form
F(t) = ò atf (x) dx ; Then F'(t) = f(t) |
|
|
|