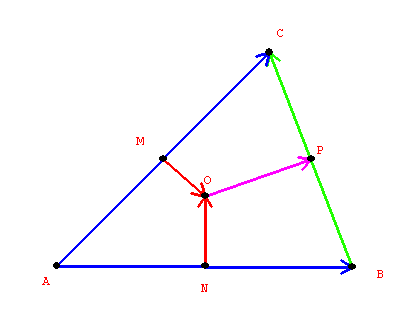
To show p is perpendicular to z it is enough to show that the inner (dot) product of p z = 0.
Now p = v +1/2 z - 1/2 v - n = 1/2 v + 1/2 (w-v) - n = 1/2 w - n , so
p z = (1/2 w - n) (w - v) = 1/2 w w - wn - 1/2 w v + n v. But since n is perpendicular to AB,
nv = 0 so we have
p z = 1/2 ww - wn - 1/2 v w =w (1/2 w - n - 1/2 v)
= w ( 1/2 w - (1/2 v + n)) =w ( 1/2 w - (1/2 w + m))= w (-m) = 0
because m is perpendicular to AC.
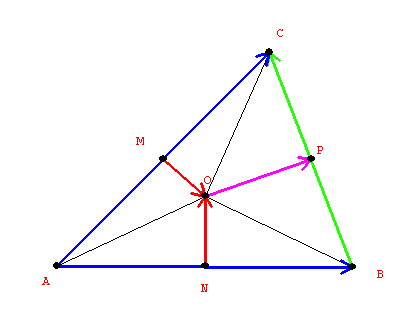
From the geometry is is clear that the point O must be equidistant from
A, B, C and thus is the center of the circle that passes through the
points A, B, and C, - the circumcenter of the triangle ABC.