
I. If possible, let the circle be greater than K.Inscribe a square ABCD, bisect the arcs AB, BC, CD, DA, then bisect (if necessary) the halves, and so on, until the sides of the inscribed polygon whose angular points are the points of division subtend segments whose sum is less than the excess of the area of the circle over
Thus the area of the polygon is greater than K.
Let AE be any side of it, and ON the perpendicular on AE from the centre 0.
Then ON is less than the radius of the circle and therefore less than one of the sides about the right angle in K. Also the perimeter of the polygon is less than the circumference of the circle, i.e. less than the other side about the right angle in K.
Therefore the area of the polygon is less than K; which is inconsistent with the hypothesis
Thus the area of the circle is not greater than.
II. If possible, let the circle be less than K
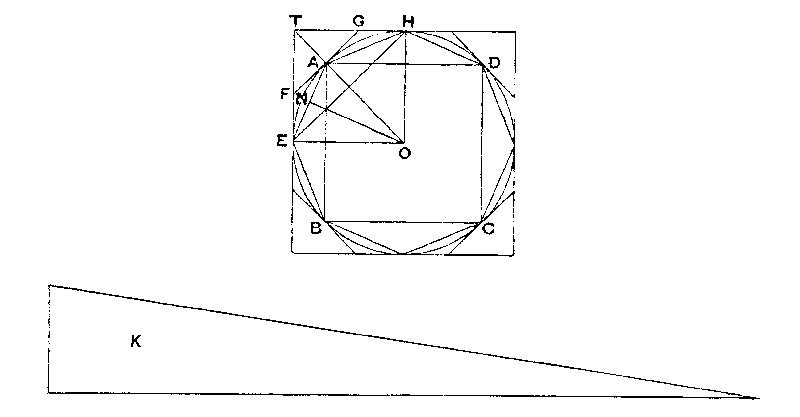
Circumscribe a square, and let two adjacent sides, touching the circle in E, H, meet in T. Bisect the arcs between adjacent points of contact and draw the tangents at the points of bisection. Let A be the middle point of the arc EH, and FAG the tangent at A.
Then the angle TAG is a right angle.
Therefore
TG > GA
It follows that the triangle FTG is greater than half the area TEAH.
Similarly, if the arc AH be bisected and the tangent at the point of bisection be drawn, it will cut off from the area GAH more than one-half.
Thus, by continuing the process, we shall ultimately arrive at a circumscribed polygon such that the spaces intercepted between it and the circle are together less than the excess of K over the area of the circle.
Thus the area of the polygon will be less than K
Now, since the perpendicular from 0 on any side of the polygon is equal to the radius of the circle, while the perimeter of the polygon is greater than the circumference of the circle, it follows that the area of the polygon is greater than the triangle K; which is impossible.
Therefore the area of the circle is not less than K.
Since then the area of the circle is neither greater nor
less than K, it is equal to it.