I.F.3. More Core Functions: Trigonometric Functions- Derivatives of the sine and cosine functions. 

© 2014 M. Flashman

  Trigonometric functions play important roles in many models. While the simplest models for populations use exponential functions, as considered in the previous section, models for sound, light, the motion of a spring, and slightly more involved models for competing populations all give rise to trigonometric functions. In Chapter VI we will investigate these models in much greater detail. For now, we’ll start our investigations with the derivatives for the sine and cosine functions.

Several problems in previous sections have investigated estimations for the derivative of the sine function.[Add references] The general problem of finding the derivative of the sine function is more difficult to derive than others we have encountered so far because the "algebra" we use is the algebra for trigonometric functions. Before going further you should review the following important parts of trigonometry: 

We begin, as we did with exponential functions, by finding the derivative of the sine and cosine functions at $0$, that is, $\sin'(0)$ and $\cos'(0)$. We'll use these derivatives to find the general derivatives of the sine and cosine at $x$, i.e., $\sin'(x)$ and $\cos'(x)$. We will investigate the derivatives of the other core trigonometric functions later in Chapter II with more relevant calculus rules.

Before making a careful argument about the values of $\sin'(0)$ and $\cos'(0)$ we can explore the graphs of these functions near $x= 0$ to gain a better sense of the slopes of their tangent lines at $x = 0.$

ch1f3_2_2011.gif
Figure 1

Graph of sine function with tangent at (0,0). 

ch1f3_2_20111.gif
Figure 2

Graph of cosine function with tangent at (0,1). 

Examining Figure 1, for the sine function, we see the slope is positive and the tangent line appears to be making an angle of about 45° with the X-axis. This suggests that its slope is close to or equal to $1$.

Examining Figure 2, for the cosine function, we see the tangent line appears to be horizontal. This suggests that its slope is close to or equal to 0.

In another informal approach, we can make a table of estimates for the values of the derivatives using the definition.

Recall that $\sin(0) = 0$, so the difference quotient simplifies to
$\frac {\sin(h)} h$.

Table I.F.3.1 gives some values for this difference quotient when $h$ is close to $0$. These estimates suggest that the limit is equal to $1$. 

$h$

$\frac {\sin(h)} h$

$h$
 $\frac {\sin(h)} h$

.5

0.95885

-.5 0.95885

.25

0.98962

-.25 0.98962

.1

0.99833

-.1 0.99833

.01

0.99998

-.01 0.99998

Table I.F.3.1
Recall that $\cos(0) = 1$, so the difference quotient simplifies to
$\frac {\cos(h) - 1} h$.

Table I.F.3.2 gives some values for this difference quotient when $h$ is close to $0$. These estimates suggest that the limit is equal to $0$.  

$h$

$\frac {\cos(h) - 1} h$

$h$ $\frac {\cos(h) - 1} h$

.5

-0.24483

-.5 0.24483

.25

-0.12435

-.25 0.12435

.1

-0.04996

-.1 0.04996

.01

-0.00500

-.01 0.00500

Table I.F.3.2


But a sampling of values in a table and inspection of the graph, while informative and supportive evidence, are not enough to prove that $\sin'(0) = 1$ and $\cos'(0) = 0$. To be assured that these limits and therefore that these derivatives are not only sensible but also correct, we need a rigorous argument that does not rely on specific values of $h$.
Proposition I.F.7. i) $\sin'(0) = D\sin(0)  = \frac d {dx} \sin(x)|_{x=0} = 1$.   
ii) $\cos'(0) = D\cos(0)  =  \frac d {dx} \cos(x)|_{x=0} = 0$.
Comment: Our proof of i) will use some geometry and careful thinking applied to the definition of the derivative. The proof of ii) will use some algebra and trigonometry, along with i). 
Proof:  i) First let's consider the case when $h > 0$ and think about $\sin(h)$ as visualized in a unit circle. See Figure 5. The sine value is represented by the vertical line segment from the X-axis to the point on the circle determined by the arc on the circle of length $h$. From this figure, at least, it seems to make sense that $\sin(h) < h$.

In Figure 5, $h$ is the length of the arc with one endpoint $Q$ and the other endpoint $P$ with coordinates $(\cos(h),\sin(h))$. Looking further at Figure 5 you can change $h$ by moving the point $P$ closer to $Q$ on the arc to see at what happens near the point $Q (1,0)$.
Check the box to add the chord $PQ$ to the figure. The length of the chord connecting $Q$ to $P$ certainly must be less than h because the shortest distance between two points is determined by the line segment connecting the points.
But the chord $PQ$ is the hypotenuse of the right triangle with its right angle at the point $R (\cos(h),0)$. Therefore the chord $PQ$ is longer than the vertical line segment $PR$, which has length $\sin(h)$. Thus, $\sin(h) < h$ when $h > 0$, so when we divide by $h$ we have $\frac {\sin(h)} h < 1$.
Now check the box  "Show Tangent to Circle" in Figure 5 and turn your attention to the right triangle formed with right angle at $Q (1,0)$, and an angle of measure $h$ at $(0,0)$. The altitude of this triangle is $\tan(h)$. [Can you explain why?$^1$]
Therefore the area of this triangle is  $\frac 1 2 \cdot 1 \cdot \tan(h) = \frac 1 2 \cdot \frac {\sin(h)} {\cos(h)}$.
 
Figure 5
                                           

But this triangle contains the sector of the circle formed by the line segment $QO$ and making an angle $h$ at $(0,0)$. This sector has an area of $\frac 1 2 \cdot h$.
Since the area of the sector is less than the area of the triangle, we have
$\frac 1 2 \cdot h <\frac 1 2 \cdot \frac {\sin(h)} {\cos(h)}$.    (2)

Since $h > 0$ and $\cos(h) > 0$ when $h$ is close to $0$, we can multiply both sides of the inequality (2) by $2\cos(h)$ and divide by $h$ to obtain the new inequality visualized in Figure 6:
$\cos(h) <  \frac {\sin(h)} h < 1$.      (4)

At this point it is time to think! (Step IV.)
Inequality (4) shows that when $h$ is close to $0$, $h>0$, $\frac {\sin(h)} h$ is between $\cos(h)$ and $1$.
Furthermore, when $ h$ is close to $0$, $\cos(h)$ is close to $1$. [Can you explain this based on Figure 1?]
Since $ \frac {\sin(h)} h$ must be even closer to $1$ than $\cos(h)$, if $h > 0$ and $h \to 0$, we see that $\frac {\sin(h)} h \to 1$. That is, 

$\lim_{h \to 0^+} \frac {\sin(h)} h = 1$.    (5)

Now what about the case when $h < 0$ and $h \to 0$?

In this case the data suggest that $\frac {\sin(h)} h = \frac {\sin(-h)}{-h}$. To see why this is true, let $k = -h$. Recall that $\sin(-h) = -\sin(h)$, so $\sin(k) = -\sin(h)$. When $h<0, k = -h > 0$, and if $h \to 0$, then $k = -h \to 0$ as well. Thus we see that
$\frac {\sin(h)} h = \frac {-\sin(h)}{-h} = \frac {sin(k)} k$.

Our previous analysis (5) showed that when $k > 0$ and $k\to 0$,  $\frac {\sin(k)} k  \to 1$.
So when $h < 0$ and $h \to 0$, $\frac {\sin(h)} h= \frac {\sin(k)} k \to 1$, i.e., 
$\lim_{h \to 0^-} \frac {\sin(h)} h = 1$.    (6)
Check this as well visually with Figure 6.
Figure 6
To summarize, in either case, with $h>0$ or with $h<0$, we find that when $h\to 0$, $\frac {\sin(h)} h \to 1$.  Therefore
$\sin'(0) = \lim_{h \to 0} \frac {\sin(h)} h = 1$.    (7)
Proof: ii) Recall that cos(0) = 1, so the difference quotient simplifies to  $\frac {\cos(0+h) - \cos(0)} h = \frac {\cos(h) - 1} h$     (8)
Now we multiply the numerator and denominator of this expression by $\cos(h) + 1$ to obtain 
$\frac {\cos(0+h) - \cos(0)} h = \frac {\cos(h) - 1} h = \frac {(cos(h) + 1)(\cos(h) - 1)}{(cos(h) + 1) h} =\frac {\cos^2(h) - 1}{(cos(h) + 1) h}=\frac {-\sin^2(h)}{(cos(h) + 1) h} = -\frac {\sin(h)} h \cdot \frac {\sin(h)}{(cos(h) + 1)}$  (9)
Now it’s time to thimk! (Step IV)
When  $h \to 0$, we saw in (7) that $ \frac {\sin(h)} h \to 1$, while $\sin(h)\to 0$ and $\cos(h)\to 1$, so $\cos(h)+ 1 \to 2$.
Putting this all together  it should make sense now that
$\cos'(0) = \lim_{h \to 0} \frac {\cos(h)-1} h = \lim_{h \to 0^-}\frac {\sin(h)} h \cdot \frac {\sin(h)}{(cos(h) + 1)} =0 $     (10)         EOP.
$^1$Hint: Let $T$ be the altitude. Then $\tan(h) = \frac T 1$.
Now that we have found the derivatives for sine and cosine at $ x =0$, it is time to think of these derivatives more generally. In Theorem I.F.9 we state these results and prove the result for the sine function. In fact, we will present two alternative proofs, each using a different trigonometric identity together with a different characterization of the derivative definition.

Here are two useful identities from trigonometry, based on the addition formulae for sine and cosine. These will be used in one of our proofs when we get to Step II (subtract) in the four step method for finding the derivative.
Lemma I.F.8:
i) $\sin(x) - \sin(a)=2 \sin(\frac 12 (x - a)) \cos(\frac12 (x + a))$.
ii) $\cos(x) - \cos(a)= - 2\sin(\frac12(x - a)) \sin(\frac12(x+a))$.

Proof: These identities arise from the addition formulae for sines and cosines. Here is the argument for i) .

        $\sin( t + u ) = \sin(t)\cos(u) + \sin(u)\cos(t)$
        $\sin( t - u ) = \sin(t)\cos(u) - \sin(u)\cos(t)$ 
so    $\sin(t + u) - \sin(t - u) = 2 \sin(u)\cos(t)$.

Now let $t = \frac12 (x + a)$ and $u = \frac12 (x - a)$ and we have $t + u = x$ while $t - u = a$.

Substitution now gives the desired result,  $\sin(x) - \sin(a)=2 \sin(\frac 12 (x - a)) \cos(\frac12 (x + a))$.
The proof of ii) is left as an exercise.     EOP
Theorem I.F.9. i) $D_x\sin(x) = \sin'(x) =\cos(x)$.
ii) $D_x\cos(x) = \cos'(x) = -\sin(x)$

Proof 1 of i)
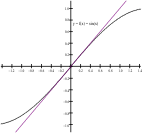
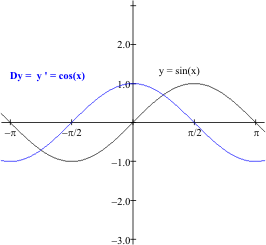
$D_x\sin(x) = \sin'(x) =\cos(x)$ using $x \to a$: $f'(a) = \lim_{x \to a}\frac {f(x)-f(a)} {x-a}$.

Remark: Using Lemma I.F.8 it is not too hard to find the general derivatives of the sine and cosine.

 We will give the argument for the derivative of the sine, leaving the proof for the cosine using the lemma as an exercise for the reader.

In finding the derivative we'll use the four step method based on the definition with $f (x) = \sin(x)$.
Moving directly to Step II (subtract), Lemma I.F.8 i) gives
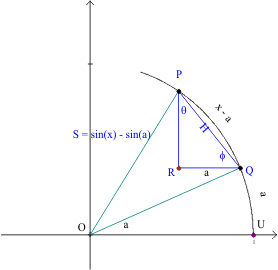
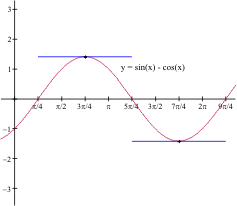
$f (x)-f (a) =\sin(x) - \sin(a)=2 \sin(\frac 12 (x - a)) \cos(\frac12 (x + a))$
Thus the difference quotient in Step III (divide) is
$\frac {f(x)-f(a)}{x-a} = \frac { \sin(x) - \sin(a)} {x-a}$
                              $= \frac {2 \sin(\frac 12 (x - a)) \cos(\frac12 (x + a))} {x-a}$.
                              $= \frac { \sin(\frac 12 (x - a))} {\frac 12 (x-a)} \cos(\frac12 (x + a)) $.

For the purpose of the Step IV analysis (Think), we first consider the factor  $\frac { \sin(\frac 12 (x - a))} {\frac 12 (x-a)}$.  Notice that when $x$ is close to $a$, the expression $\frac 12 (x- a)$ is close to $0$. Think of $\frac 12 (x- a)$ as a number which we can call $h$. Now the factor is  $\frac { \sin(h)} h$.

It's time to think! When $x \to a$ , $h \to 0$. Our work in finding $\sin'(0)$ showed that $\frac { \sin(h)} h \to 1 $,  or equivalently,  $\frac { \sin(\frac 12 (x - a))} {\frac 12 (x-a)} \to 1$.

Using the definition of the cosine function on the unit circle should make it sensible to see that when $x \to a$ , $\frac 12 (x+ a) \to a$, and thus $\cos( \frac 12 (x + a)) \to \cos(a)$.

Putting this all together, we have

$f'(a) = \lim_{x \to a}\frac {f(x)-f(a)} {x-a}$
               $=\lim_{x \to a} \frac { \sin(x) - \sin(a)} {x-a}$                                          
               $= \lim_{x \to a}\frac { \sin(\frac 12 (x - a))} {\frac 12 (x-a)} \cos(\frac12 (x + a)) $                                   
               $= \cos(a)$
So replacing $a$ with $x$ we have the general result: $D_x\sin(x) = \sin'(x) =\cos(x)$.  EOP.

Proof 2 of i)
$D_x\sin(x) = \sin'(x) =\cos(x)$ using $h \to 0$:
$f'(a) = \lim_{h \to 0}\frac {f(a+h)-f(a)} {h}$.

Remark: In this proof we make use of the addition identity:

$\sin(A+B) = \sin(A)\cos(B) + \cos(A)\sin(B)$

In finding the derivative this time we'll use the four step method based on the definition with $f (x) = \sin(x)$.
Moving directly to Step II (subtract),the addition identity for the sine gives
        $f(a+h)-f(a) = \sin(a+h) - \sin(a)$
                          $= \sin(a)\cos(h) + \cos(a)\sin(h) - \sin(a)$
                          $= \cos(a)\sin(h) + \sin(a) [\cos(h) -1]$.

Thus the difference quotient in Step III (divide) is
        $\frac {f(a+h)-f(a)}h = \frac { \sin(a+h) - \sin(a)} h$
                                        $= \frac { \cos(a)\sin(h) + \sin(a) [\cos(h) -1]} h$.
                                        $= \cos(a)\frac { \sin(h) }h + \sin(a) \frac {[\cos(h) -1]} h$.

For the purpose of the Step IV analysis (Think), we first consider the term $ \cos(a)\frac { \sin(h) }h$.
Notice that when  $h$ is close to $0$, our work in finding $\sin'(0)$ showed that  $\frac { \sin(h) }h \to 1$, so it should make sense that $ \cos(a)\frac { \sin(h) }h  \to \cos(a)$.

Now consider the term $\sin(a) \frac {[\cos(h) -1]} h$ . Our recent work in finding $\cos'(0)$ showed that $\frac {\cos(h)-1} h \to 0$, so it should make sense that  $\sin(a) \frac {[\cos(h) -1]} h \to 0$ .

Putting this all together, we have

$f'(a) = \lim_{h \to 0}\frac {f(a+h)-f(a)} {h}$                                              
                     $= \lim_{h \to 0} \frac { \sin(a+h) - \sin(a)} h$                                               
                                                            $= \lim_{h \to 0}  \cos(a)\frac { \sin(h) }h + \sin(a) \frac {[\cos(h) -1]} h$
$= \cos(a) + 0$.                                                 

So replacing a with x we have the general result: $D_x\sin(x) = \sin'(x) =\cos(x)$.   EOP.                              

   

Proof of ii) using $h\to 0$:
Remark: In this proof we make use of the addition identity:
$\cos(A+B) = \cos(A)\cos(B) - \sin(A)\sin(B)$

We'll use the four step method based on the definition with $f (x) = \cos(x)$.
Moving directly to Step 2 (subtract),the addition identity for the sine gives
        $f(a+h)-f(a) = \cos(a+h) - \cos(a)$
                          $= \cos(a)\cos(h) - \sin(a)\sin(h) - \cos(a)$
                          $=  -\sin(a)\sin(h) + \cos(a) [\cos(h) -1]$.
Thus the difference quotient in Step 3 (divide) is
     $\frac {f(a+h)-f(a)}h = \frac { \cos(a+h) - \cos(a)} h$
                                        $= \frac { -\sin(a)\sin(h) + \cos(a) [\cos(h) -1]} h$.
                                        $= -\sin(a)\frac { \sin(h) }h + \cos(a) \frac {[\cos(h) -1]} h$.
For the purpose of the Step 4 analysis (Thimk), we first consider the term .

For the purpose of the Step IV analysis (Think), we first consider the term $ -\sin(a)\frac { \sin(h) }h$.
Notice that when  $h$ is close to $0$, our work in finding $\sin'(0)$ showed that  $\frac { \sin(h) }h \to 1$, so it should make sense that $ -\sin(a)\frac { \sin(h) }h  \to -\sin(a)$.

Now consider the term $\cos(a) \frac {[\cos(h) -1]} h$ . Our recent work in finding $\cos'(0)$ showed that $\frac {\cos(h)-1} h \to 0$, so it should make sense that  $\cos(a) \frac {[\cos(h) -1]} h \to 0$ .

Putting this all together, we have

$f'(a) = \lim_{h \to 0}\frac {f(a+h)-f(a)} {h}$                                              
                     $= \lim_{h \to 0} \frac { \cos(a+h) - \cos(a)} h$                                               
                  $= \lim_{h \to 0}  -\sin(a)\frac { \sin(h) }h + \cos(a) \frac {[\cos(h) -1]} h$
$= -\sin(a) + 0$.                                                                           

So replacing a with x we have the general result: $D_x\cos(x) = \cos'(x) = -\sin(x)$.             EOP.

Summary of derivatives for sine and cosine function

ch1f3_2_20114.gif
Figure 9 Graph of Sine Function
and its Derivative.  

ch1f3_2_20115.gif
Figure 10 Graph of Cosine Function
and its Derivative.

Graphical Interpretation of the Sine and Its Derivative: Note that the value of the sine’s derivative is $0$ when $x$ is $ \pm \frac {\pi} 2$. For the graph of the sine at these same $x$’s, it seems the corresponding tangent lines would be horizontal.

Graphical Interpretation of the Cosine and Its Derivative: Note that the value of the cosine’s derivative is $0$ when $x$ is $0$ and $\pm \pi$. For the graph of the cosine at these same $x$’s, it seems the corresponding tangent lines would be horizontal..


Example I.F.10. Find all numbers $a$ between $0$ and $2\pi$ where the tangent line for the graph of $y = \sin(x) - \cos(x)$ is horizontal.

Solution: For the tangent line at $x = a$ to be horizontal, it must have a slope of $0$. So we are looking for numbers $a$ between $0$ and $2\pi$ where the derivative of $y$ is $0$ at $x = a$. Now from the derivative calculus we have that  $\frac{dy}{dx} = \frac d{dx}\sin(x) - \frac d{dx} \cos(x) = \cos(x) +\sin(x)$ . Setting this derivative to $0$ at $x = a$, we see that $\cos(a) + \sin(a) = 0$. Solving this trigonometric equation we find that for this value of $a$, $\cos(a) = - \sin(a)$, and thus $\tan (a) = -1$. So for the tangent line at $x = a$ to be horizontal with $a$ between $0$ and $2\pi$, it must be that $a$ is either $\frac 34 \pi$ or $\frac 74 \pi$. See Figure 11.

ch1f3_2_20116.gif
 
Figure 11

I.F.3.a [Optional] The Derivative of The Sine: A More Geometric View.

Here is an alternative demonstration that $\sin’(a) = \cos(a)$.
Consider sin(x) and cos(x) as defined on the unit circle. That is, an arc on the unit circle starting at (1,0) and having length x has its endpoint with coordinates (cos(x), sin(x)). Similarly the arc of length a on the unit circle has its endpoint with coordinates (cos(a), sin(a)) .

When x is close to a , the value of sin(x) - sin(a) represents the length of the vertical side S of a right triangle PQR with vertices P(cos(x),sin(x)), Q (cos(a),sin(a)) and R (cos(x),sin(a)). [See Figure 12.] The difference x-a represents the difference in the lengths between arc x and arc a. When x is very close to a, x - a is approximately equal to the length of the hypotenuse H of triangle PQR, i.e, the length of the chord PQ.

Thus $\frac {\sin(x)-\sin(a)} {x-a}$ is approximated by S/H which is the cosine of the angle RPQ (formed at P) which we'll call θ, i.e.,$\frac {\sin(x)-\sin(a)} {x-a} \approx \frac SH= \cos(\Theta)$.

 Now θ depends on the choice of x in a very useful fashion. When x is very close to a, the angle PQO (formed at Q) is almost a right angle. θ is the complement of the angle PQR labeled φ in Figure 12. Since RQ is parallel to the horizontal axis, the angle RQO has the same measure as angle QOU. So these two angles are both labeled a in Figure 12.
ch1f3_2_20117.gif


Figure 12

Now we notice that when x is very close to a, angle RQO is close to being the complement of the angle PQR labeled φ, and thus the angle θ has a measure that is close to a. So, when x is close to a, cos (θ) is close to the cos(a).

Thus as x→a and we see that sin'(a) = cos(a).                                                                 EOP




Exercises I.F.3.

1.    Find $\frac{dy}{dx}$ when
    a.    $y = 5 \sin(x) - 3 \cos(x)$;            $y = \ln(x^2) + \sin (x)$
    b.   $ y = \cos(x) - 5x - 3$ ;       $ y = 3 \sin (x) +  \frac 1x$
2.    Find all $x$ where $f'(x) = 0$  when
    a.    $f(x) = \sin(x)$             d.     $f(x) = \sin(x) + x$
    b.    $f(x) = \cos(x)$            e.    $f(x) = \cos(x) - x$
    c.    $f(x) = \sin(x) + \cos(x)$
3.    Consider $F(x) = \sin(x)$ is a probability distribution for the random variable $X$ on the interval $[0, π/2]$. Find the probability density at $x=π/4, π/6,$ and $π/3$. Explain briefly why the values for $X$ are more likely to fall closer to $π/6$ then to $π/4$ or $π/3$.
4.    Prove Lemma ii). Use this to prove Theorem I.F.9.ii).
5.    Give a geometric analysis for showing $\cos'(x) = -\sin(x)$.
    [Hint: Discuss why $\frac{\cos(x)-\cos(a)}{x-a} \approx -\sin(\Theta)$. How do you explain the "$-$" in the geometry?] Now complete the argument showing that $\frac{\cos(x)-\cos(a)} {x-a}\approx -\sin(θ) \to -\sin(a)$.
6.    Challenge: Give a geometric analysis for showing $\tan'(x) = sec^2(x)$.
    [Hint: Discuss why $\frac{tan(x)-tan(a)} {x-a} \approx \sec^2(a)$. How do you explain the term $\tan(a)$ in the geometry?] Now complete the argument.
7.    Challenge: Give a geometric analysis for showing $\sec'(x) = \sec(x)\tan(x)$.
    [Hint: Discuss why $\frac{\sec(x)-\sec(a)}{x-a} \approx \sec(a)\tan(a)$. How do you explain the term $\sec(a)$ in the geometry?] Now complete the argument.

8.    Find a function P where $ P'(x) = f(x)$ for the  following:
    a.    $f(x) = 5 \cos(x) - \frac 3{x^2} + 2x^{ 3/5}$    b.   $ f(x) = 2 \sin(x) - 3x^2 + 2x^{ 5/7}$ .   
9.    Explain why $\frac {d\sin(-x)}{dx} = -\cos(x)$ but $\sin'(-x)=\cos(x)$ and $\frac {d\cos(-x)}{dx} = -\sin(x)$ while $\cos'(-x)=\sin(x)$..
Discuss these results with regard to the graphical interpretation of these derivative.
10.    Use the addition identity to prove that
    a.     $\sin(x+π/2) = \cos(x); \sin(x+π) = -\sin(x)$;
    b.     $\cos(x+π/2) =-\sin(x); \cos(x+π) =-\cos(x)$.
Use the identities in parts a) and b) to explain why
    c.   $ \frac {d\sin(x+π/2)}{dx} = -\sin(x); \frac {d\sin(x+π)}{dx}= -\cos(x)$;
    d.    $\frac{d\cos(x+π/2)}{dx} =-\cos(x); \frac{d\cos(x+π)}{dx} = \sin(x)$.
 Discuss these results with regard to the graphical interpretation of these derivative.