From the Math History web site: http://www-history.mcs.st-andrews.ac.uk/history/HistTopics/The_four_colour_theorem.html

Article by: J J O'Connor and E F Robertson JOC/EFR September 1996

However the final ideas necessary for the solution of the Four Colour Conjecture had been introduced before these last two results. Heesch in 1969 introduced the method of discharging. This consists of assigning to a vertex of degree i the charge 6-i. Now from Euler's formula we can deduce that the sum of the charges over all the vertices must be 12. A given set S of configurations can be proved unavoidable if for a triangulation T which does not contain a configuration in S we can redistribute the charges (without changing the total charge) so that no vertex ends up with a positive charge.

Heesch thought that the Four Colour Conjecture could be solved by considering a set of around 8900 configurations. There were difficulties with his approach since some of his configurations had a boundary of up to 18 edges and could not be tested for reducibility. The tests for reducibility used Kempe chain arguments but some configurations had obstacles to prevent reduction.

The year 1976 saw a complete solution to the Four Colour Conjecture when it was to become the Four Colour Theorem for the second, and last, time. The proof was achieved by Appel and Haken, basing their methods on reducibility using Kempe chains. They carried through the ideas of Heesch and eventually they constructed an unavoidable set with around 1500 configurations. They managed to keep the boundary ring size down to less than or equal to 14 making computations easier that for the Heesch case. There was a long period where they essentially used trial and error together with unbelievable intuition to modify their unavoidable set and their discharging procedure. Appel and Haken used 1200 hours of computer time to work through the details of the final proof. Koch assisted Appel and Haken with the computer calculations.

The Four Colour Theorem was the first major theorem to be proved using a computer, having a proof that could not be verified directly by other mathematicians. Despite some worries about this initially, independent verification soon convinced everyone that the Four Colour Theorem had finally been proved. Details of the proof appeared in two articles in 1977. Recent work has led to improvements in the algorithm.

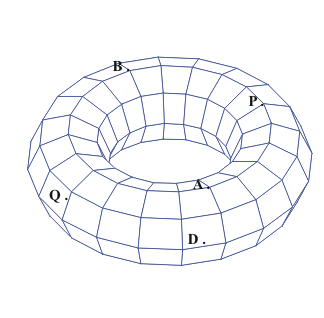
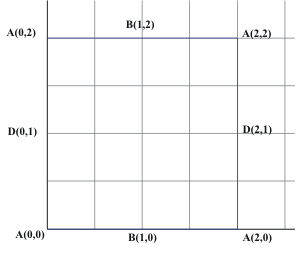
What about graphs on the Torus?
We have a connected graph on the torus with one vertex, two edges and only one region. But this information does not match for the euler formula for the plane or the sphere. SO.. the torus must be topologically different from the sphere or the plane!
In fact for the torus we see that it is possible for V+R= E   or  V-E+R= 0

We learned about (and proved) Euler's Formula for the plane or the sphere. What can we say about a formula for the torus or the Klein bottle?

Surfaces:Mark Sudduth's web page of surfaces.[ A physics master's degree student at UT, Arlington.

What is a surface?
Bounded, unbounded:
Closed, open:
With or without boundary:
Orientable or Non-orientable: we considered the moebius band and the Klein Bottle as examples of non-orientable surfaces.
Can be realized (imbedded) in a plane, in 3 space, in 4 space.
Can be visualized (immersed) in ...


Examples:A closed disc, an open disc, a plane, an annulus- cylinder, a mobius band;

 

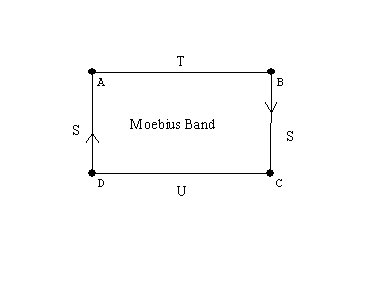
Experiments with the mobius band. Drawing a curve along the center of the band we cover both "sides." Cutting along that curve the band does not fall apart, but gets twice as long!

a sphere,
a torus

 

a Klein bottle

A javaview visualization of the Klein bottle

,

the projective plane... Why is this a closed and bounded surface?

;

A sphere with a cross cap .

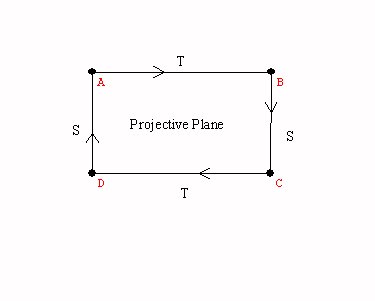
Activity:Graphs on the torus.
Games and puzzles on the torus and the klein bottle.

From the Fun Fact files, hosted by the Harvey Mudd College Math Department ,  Unbelievable Unlinking Figure 1 Figure 2 Imagine that the two objects in Figure 1 are solid (with thickness) and made of very flexible and stretchy rubber. Question: is it possible to deform one object into the other in a continuous motion (without tearing or cutting)? Surprise answer: Yes!! Hint: it is important that the object is solid and has thickness; this transformation cannot be done with a one-dimensional piece of string. It is also not possible to do this with a piece of rope because even though the rope has thickness, it is not flexible or "stretchy" enough. See below for an explanation and animated gif. Or, don't scroll down if you want to think about it a while! The Math Behind the Fact: One way to do this is the following. Widen one of the loops and move one of its handles along the stem between the two loops to the other loop and push it through the hole so that the two loops become unlinked. The reference contains a sequence of pictures of this transformation. Graeme McRae has generously contributed the animated gif in Figure 2, showing another solution to this problem! (Thank you, Graeme!) Here is the original picture:

Visualizations of surfaces by flattened - cut apart models.
A cylinder, a mobius band, the torus, the Klein bottle, the projective plane.


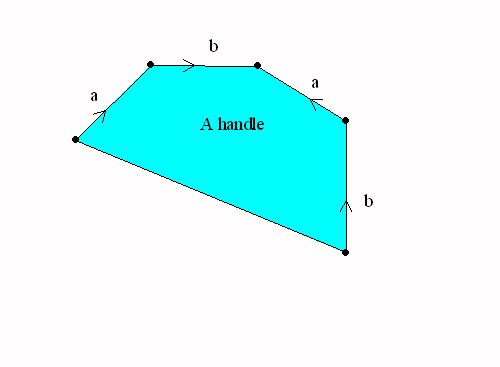
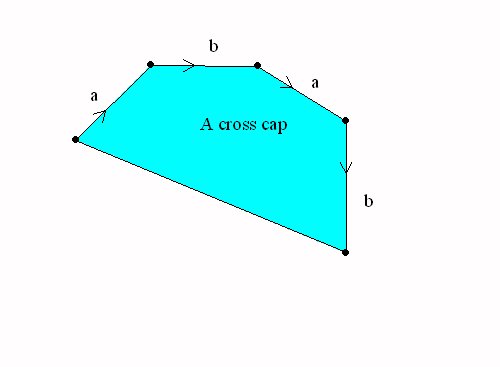
Closed Surfaces: Handles and cross-caps  attached to the sphere.

A sphere with a handle = a torus	A Sphere with a cross cap = the projective plane

The Topological Classification of "closed surfaces."

Every connected closed and bounded surface is topologically equivalent to a sphere with handles and crosscaps attached.


Proof....

This classification determines the euler characteristic of each surface.
If the surface is orientable, it is a sphere with n handles, so V-E+R = 1 - 2n +1 = 2-2n.  For example the torus has euler characteristic 2-2*1=0.
If the surface is non-orientable, then  is it a sphere with k crosscaps and n handles, so the euler characteristic is V-E+R = 1 - (k+2n) +1 =2 -2n -k.
Notice that a sphere with two cross caps has euler characteristic 0, the same as the torus. But this was the euler characteristic of the Klein Bottle. So we should be able to recognize the Klein bottle as a sphere with two cross caps.
This can be done by a single normalization of one pair of edges with the same  orientation.

---

Other interest in surfaces: Examples
Ways to think of surfaces : cross-sections/ projections/moving curves/ using color to see another dimension.

Generalization of surfaces are called "manifolds".  cross sections / projections/ moving surfaces-solids.
"minimal surfaces" (FAPP video?)
Transforming surfaces: "turning the sphere inside out." video

---