• Reflective symmetry: BI LATERAL SYMMETRY   
  
  T  C  O   0    I   A 
• Folding line: "axis of symmetry"
  

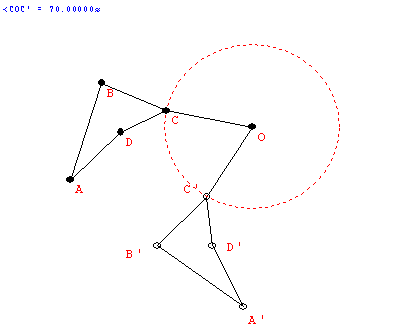
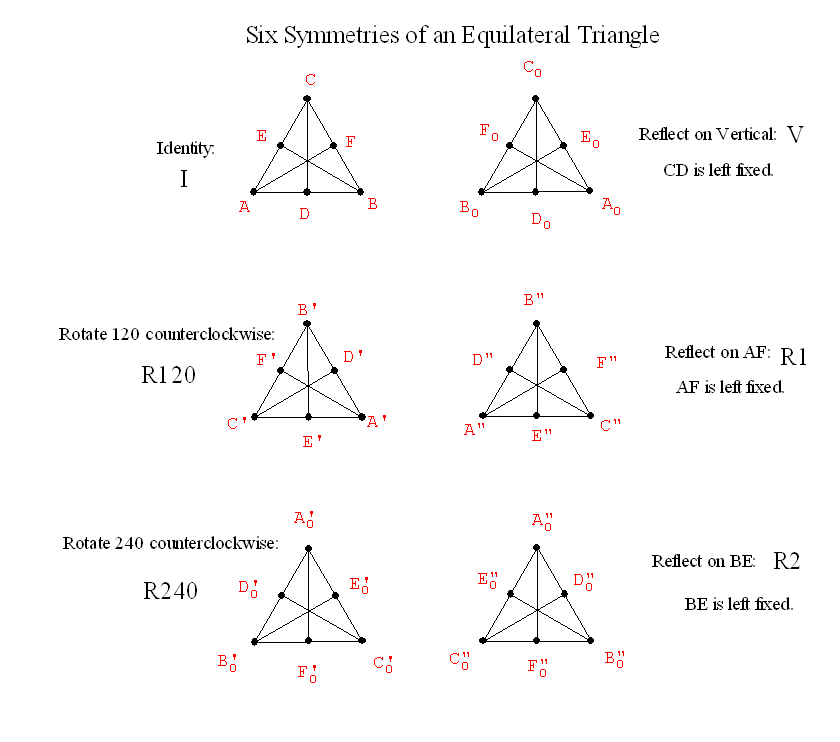
• The "flip."
  
• The "mirror."
• 
  
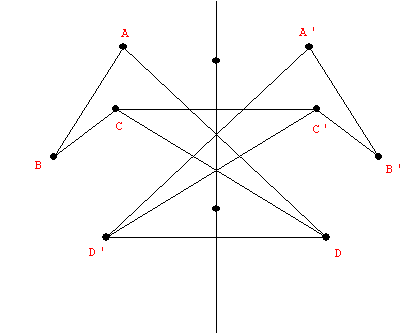
• R(P) = P'  : A Transformation. Before: P .... After : P'
• If P is on the line (axis), then R(P)=P. "P remains fixed by the reflection."
• If P is not on the axis, then the line PP' is perpendicular to the axis and if Q is the point of intersection of PP' with the axis then m(PQ) = m(p'Q).
  
  
  
• Definition: We say F has a reflective symmetry wrt a line l if  there is a reflection  R about the line l where  R(P)=P' is still an element of F for every P in F....i.e.. R (F) = F. l is called the axis of symmetry.
• Examples of reflective symmetry:
  Squares...  People
• 
  

• ---

• Rotational Symmetry.
• Center of rotation. "rotational pole" (usually O) and angle/direction of rotation.
  
• The "spin."
• 
  
• R(P) = P' : A transformation
• If O is the center then R(O) = O.
• If the angle is 360 then R(P) = P for all P.... called the identity transformation.
• If  the angle is between 0 and 360 then only the center remains fixed.
• For any point P the angle POP'  is the same.
• Examples of rotational symmetry.
  

•  Now... what about finding all the reflective and rotational symmetries of a single figure?
  

  ---

  
  
• Symmetries of playing card.... classify the cards by having same symmetries.
  
  
  Notice symmetry of clubs, diamonds, hearts, spades
• 
  

  Organization of markers.

  ---

  Symmetries of an equilateral triangle:
  
• 

• What about combining transformations to give new symmetries:

Think of a symmetry as a transformation, for example, V will mean reflection across the line that is the vertical altitude of the equilateral triangle.

Then let's consider a second symmetry, called R=R120, which will rotate the equilateral triangle counterclockwise about its center O by 120 degrees.

We now can think of first performing V to the figure and then performing R to the figure.  
We will denote this V*R... meaning V followed by R.
[Note that order can make a difference here, and there is an alternative  convention for this notation that would reverse the order and say that R*V means V followed byR.]
Does the resulting transformation also leave the equilateral  covering the same position in which it started?

V*R     =   R2 ?

If so it is also a symmetry.... which of the six is it?

What about other products?  This gives a  "product" for symmetries.
If S and R are any symmetries of a figure then S*R is also a symmetry of the figure.

A "multiplication" table for Symmetries:

*	Id	R120	R240	V	G=R1	H=R2
Id	I
R120		R240		R1
R240		I		R2
V		R2	R1	I		R120
G=R1					I
H=R2						I

Do Activity. This shows that R240*V = R1

  This "multiplicative" structure  is called the Group of symmetries of the equilateral triangle.

Given any figure we can talk about the group of its symmetries.
Does a figure always have at least one symmetry? .....

Yes... The Identity symmetry.
Such a symmetry is called the trival symmetry.

So we can compare objects for symmetries....
how many?
does the multiplication table for the symmetries look the same in some sense?