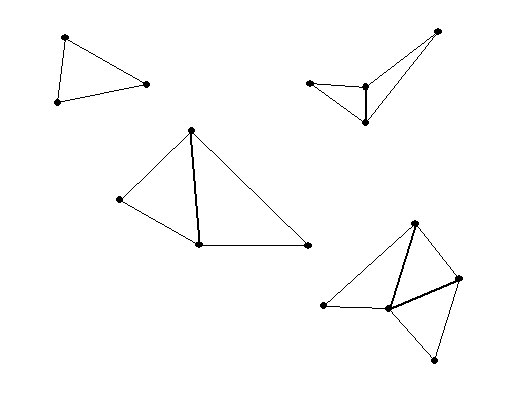
When n = 3 this is a triangle, n=4, a quadrilateral, or when n= 5, a pentagon.

The sum of the measures of the interior angles of a triangle is 180 degrees.
Question:What about a quadrilateral? and a pentagon?  or an n sided polygon  ( an "n -gon")?

 

From the figure we saw that for a quadrilateral (n =4), which can be dissected into two triangles,
the sum is 2*180= 360 degrees.
And for a pentagon (n=5) which can be dissected into 3 triangles, the sum is 3*180=540 degrees.

A regular  polygon is a polygon where the sides are all of equal length and the angles are all congruent (or of equal measure).

For a triangle, the individual angle is __180/3 =_60____ degrees.
For a square, the individual angle is ___360/4=90_____ degrees.
For a regular pentagon.... ____3*180/5 = 540/5 =108__  degrees.

Now for a HEXAGON (6 sides) the sum of the angles is
                             ____720___ degrees.
So ... for a REGULAR HEXAGON,  the individual angle is  4*180/6 =720/6 =120________ degrees.

• Dissection of the plane--- Tilings of the plane.

• One polygonal Tile: Quadrilateral Activity. (related to Assignment due next class!)
• An on-line tool for making tilings of the plane
• Regular and semiregular Tilings of the plane.
• A tiling is a regular tiling if(i)it has a single tile shape that is a regular polygon and (ii) the vertices and edges of the tiles coincide (no overlapping edges)
• A tiling is a semi-regular tiling if (ii) each tile shape is a regular polygon, (ii) the vertices and edges of the tiles coincide (no overlapping edges) and (iii) every vertex has the same polygon types arranged around it.
  
• Wingeometry download! and demonstrate tesselations.
• Naming tilings (Math Forum)
• The numbers represent the number of sides in the poygons.
• The order indcates the order in which the poygons are arranged about a vertex.
  
• Local considerations about a vertex. The sum of the angles must equal 360 degrees.
• 4.1  Ex. 3. How many tiles around single vertex: 3,4,5,6,7,8?...
• How can there be 6? Only one way: 3-3-3-3-3-3   (6*60= 360)
• Why not 7? If 7 or more tiles aroung a single vertex the sum of the angles must exceed 360 degrees.
• 4.1  Ex. 4. Can there be 4 different tiles around a single vertex? Not if they are all different since 60+90+108+120 = 378 >360.
• 4.1  Ex. 5. If there are 4 tiles around a vertex then ....At least two of the tiles must have the same number of sides.
• Arithmetic for vertices.

Example: Three regular polygons about a vertex with n , k, and p sides.

(180 - 360/n) + (180 - 360/k) + (180 - 360/p) = 360

3*180 -360( 1/n+1/k+1/p)= 2*180


1*180 = 360( 1/n+1/k+1/p)

So, for example, n=3, k=4 and p= 5 is not possible since

Number of polygons  around a vertex	Equation for angle sum = 360	Equivalent Arithmetic equation	Solutions to the arithmetic equations.
3: n , k, p	180 - 360/n+180 - 360/k+180 - 360/p = 360	1/n+1/k+1/p =1/2	6 6 6 5 5 10 4 5 20 4 6 12 4 8 8 3 7 42 3 8 24 3 9 18 3 10 15 3 12 12
4:  n, k, p, z	180 - 360/n+180 - 360/k+180 - 360/p 180 - 360/z = 360	1/n+1/k+1/p +1/z =2/2 =1	4 4 4 4 3 3 4 12 3 3 6 6 3 4 4 6
5:  n, k, p, z, w	180 - 360/n+180 - 360/k+180 - 360/p+180 - 360/z+180 - 360/w = 360	1/n+1/k+1/p +1/z+1/w =3/2	3 3 3 3 6 3 3 3 4 4

• Local consideration about a polygon:
• Examples: If there is an equilateral triangle involved with 2 other polygons, then the other two ploygons must have the same number of sides. Because: if there were two different polygons aroung the triangle, then on vertex would not have all three polygons sharing that vertex. (such as 3-10-15)
• Similar considerations can eliminate tilings using a single pentagon and two other distinct tiles. (such as 4-5-20).
  
• Semiregular Tilings: global results!
  Look at the results using wingeometry.
  
• Student lesson (Math Forum) a place for further explorations on-line.