- Measurement and the Pythagorean
Theorem (PT)
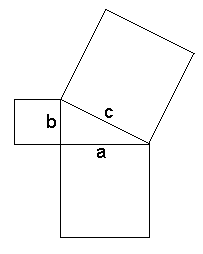
a2 + b2 = c2
How can one distinguish the
sphere from a plane (Flatland) based solely on experiences
on the surface?
How can one distinguish the
sphere from a torus based solely on experiences on the surface?
Use shadows?: look at shadows at the same time of
day? This is a "local" feature of the surface.
Observe "curvature"? This is also a local property.
Circumnavigate (Global)?: Go West -> return
from the East, then go North-> return from the south.
On a sphere: there will always be 2 points of intersection
of the curves determined by the two routes.
On a torus: There will be only one point of intersection
of the two routes.
plane: Go West -> you keep going... there seems
to be no return???
Other issues: What about strange gravity? Finding an edge? How do you know
when you start?

Show video on PT- (Video Number 950) Put on reserve in library!
Background: Similar triangles
Area of triangles = 1/2 bh
Area of parallelogram= bh
Scaling: a linear scale change of r gives area change of factor r^2.
3 questions: running, moat, wind power...
Proof of the PT: Similar right triangles: c= a2 /c + b2 /c .
applications and other proofs.
Prop. 47 of Euclid.
Dissection Proof.
Prop 31 Book VI Similar shapes.
Simple proof of PT using similar triangles of the triangle.
Use in 3 dimensional space.